|
Number & Operations for Teachers Copyright David & Cynthia Thomas, 2009 |
||||
|
Mathematical Connections
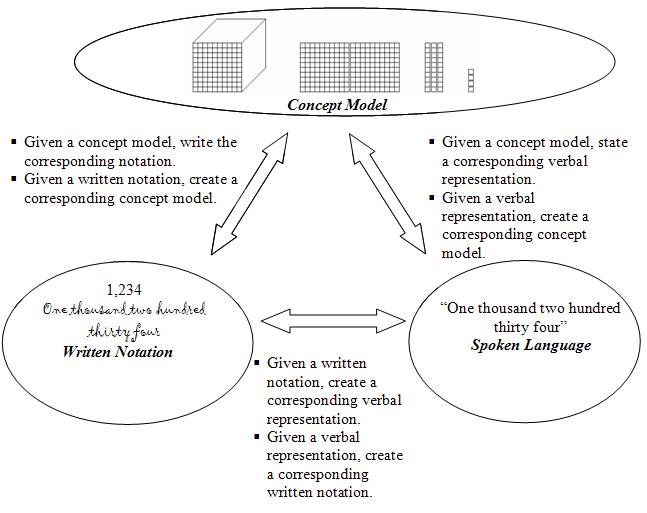
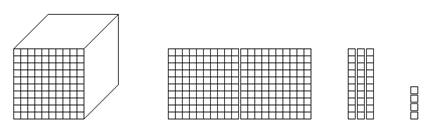
Figure 1.3: Asking the Right Questions about Essential Connections Mathematics is more than a collection of facts. It is a system of thought with its own language for explaining complex relationships, procedures, and phenomena. From their earliest experiences with mathematics and throughout their mathematical education, students should develop fluency in the use of concept models, written notations and algorithms, and the spoken language of mathematics. Figure 1.3 shows written, spoken, and graphical representations for the number 1,234. Also shown are sample conversion tasks that a teacher might use as prompts in a whole class discussion. Example 1.6 demonstrates the sort of exchange that might occur between teacher and student to practice this sort of fluency. Example 1.6 A teacher writes the number 1,234 on the board and asks the class to · Say the number using standard mathematical vocabulary · Write the number using words rather than numerals · Model the number using base ten blocks Solution 1.6 The correct responses are · In spoken form, “One thousand two hundred thirty four” ; · In written form, One thousand two hundred thirty four; and ·
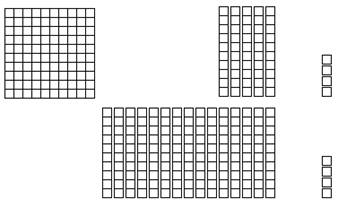
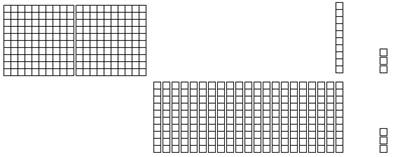
While fluency of this sort greatly facilitates mathematical communication, fluency is only a means to an end … understanding. In using multiple representations for new mathematical concepts and procedures, the ideas themselves become more memorable because of the richness of the connections between concepts, oral language, and written notations. Approached in this manner, sense-making becomes a normal and rewarding activity in the teaching and learning of mathematics. When mathematics makes sense, anxiety and fear are banished. Among the many concepts in primary grades mathematics, perhaps the most important is that of place value as it applies to regrouping (carrying and borrowing) when adding and subtracting whole numbers. A helpful background for the introduction of this topic involves the use of base ten blocks to create alternative representations for whole numbers. For instance, the number 154 may be decomposed as 1(hundred) + 5(tens) + 4(ones) or as 15(tens) + 4(ones). Using base ten blocks, these decompositions may be modeled as shown in Figure 1.4. Notice that, while the base ten block representations are clearly different, the standard written forms are indistinguishable. [Underlining has been added to denote the number of tens used in each model.]
Figure 1.4: Alternative Decompositions Example 1.7 Using base ten blocks, create conventional and an alternative representations for the number 213. Solution 1.7
|
||||
|
|