|
Number & Operations for Teachers Copyright David & Cynthia Thomas, 2009 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Modeling the Meaning of Decimal
Numbers The numeration system used to represent whole numbers and integers may be extended to represent decimal numbers. In this extension, columns to the right of the decimal point are associated with successive negative powers of ten (See Table 6.1).
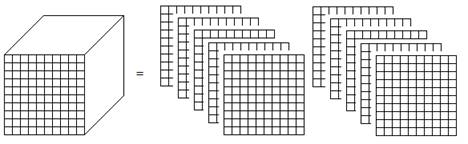
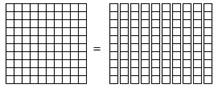
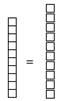
Table 6.1: Notations for representing the decimal number 4321.234 In this representation, adjacent columns to the right of the decimal point are related to one another in the same manner as adjacent columns to the left of the decimal point: Any non-zero numeral, regardless of its position, represents a quantity ten times that associated with the same numeral written in the column immediately to its right. For instance, the first column to the right of the decimal point is associated with multiples of one-tenth, written in Table 6.1 as 0.1 or 10-1. The column immediately to its right is associated with multiples of one-hundredth, written as 0.01 or 10-2. Using these notations, the relationship between the columns may be written as 10(0.01) = 0.1 or as 10(10-2) = 10-1. A similar relationship exists between every pair of adjacent columns, regardless of their positions relative to the decimal point.
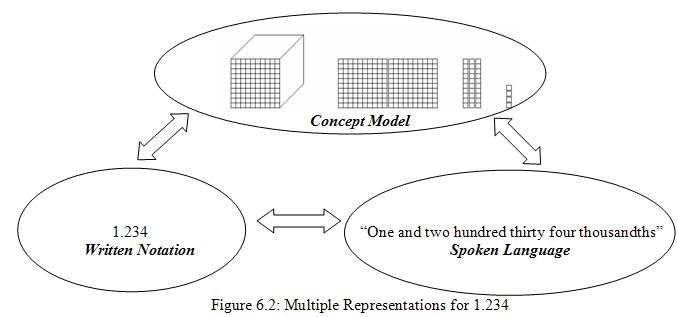
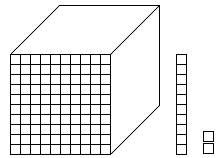
While decimal and exponential notations may satisfy university students, some other justification is needed when explaining these relationships to young learners. Fortunately, these relationships may be modeled using base ten blocks, the same tool used in Chapter One to model whole numbers. Adapting base ten blocks to model decimal numbers, the block (previously used to represent 1000) is redefined to represent a one. The lines inscribed on the block suggest that the one may be subdivided into smaller parts. These parts are named tenth, hundredth, and thousandth and are related to one another as seen in Figure 6.1.
Figure 6.1: Concept Model for Decimal Numbers Using this concept model, one may represent decimal numbers using graphical, written, and spoken representations. Figure 6.2 shows these representations and their connections. Through direct instruction and practice, all students should become fluent in the use of multiple representations of this sort.
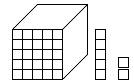
Example 6.1 Using base ten blocks, model the following decimal numbers: § 0.103 § 1.012 Solution 6.1 § § A similar approach may be used to model “decimal” number in other systems of numeration. For instance, Table 6.2 shows an expanded notation for representing the number 4321.234five. In this representation, columns to the right of the decimal point are associated with successive negative powers of five. An important insight associated with this demonstration is that there is nothing special about the base ten numeration system relative to its capacity to represent numbers between zero and one. Numbers between zero and one may be represented in other systems using comparable notations.
Table 6.2: Notations for representing the decimal number 4321.234five Example 6.2 Using base five blocks, model the following numbers: § 0.103 five § 1.012 five Solution 6.2 § § A natural question arises whenever numbers from different numeration systems are compared: Which number represents the larger quantity? As a first step in considering this question, Table 6.3 compares different notations of the numbers 0.111, 0.111nine, 0.111eight, 0.111seven, and so on.
Table 6.3: Exponential vs. Fraction Notations In Table 6.4, the first column repeats same numbers seen in the first column of Table 6.3. The next three columns present the base ten value associated with each column of these numbers. The last column presents each number’s overall value in base ten notation. Comparing these values, it is clear that the value associated with the number 0.111 increases as the base defining its numeration system becomes smaller. The same effect is also seen in the previous three columns. The basis for this effect lies in the fact that smaller bases are associated with smaller denominators in each numbers fraction notation (see Table 6.3). In any fraction, as the denominator decreases, the value of the fraction increases. For instance, 1/4 < 1/3 < 1/2. Consequently, as the base of the numeration system gets smaller, the value associated with each column in the representation 0.111base gets larger, as does that of the number itself.
Table 6.4: Comparing the value of 0.111 in different systems of numeration The opposite effect is observed when comparing the value of the whole number 111 in the same numeration systems (See Table 6.5). That is, as the base of the numeration system increases, the value associated with each place increases. For instance, 22 < 32 < 42, and so on. Consequently, the overall value of each representation increases as the value of the base increases.
Table 6.5: Comparing the value of 111 in different systems of numeration |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||