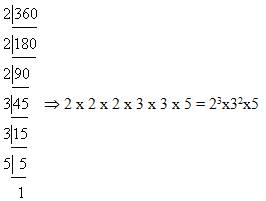|
Number & Operations for Teachers Copyright David & Cynthia Thomas, 2009 |
||||||
|
Greatest Common
Factor, Prime Factorization, and Least Common Multiple The factors of 12 are {1, 2, 3, 4, 6, 12) and the factors of 18 are {1, 2, 3, 6, 18}. Comparing the factors of 12 to the factors of 18, several common factors are found, {2, 3, 6}. The largest of these common factors is called the greatest common factor (GCF). The greatest common factor of 12 and 18 is 6, written GCF(12,18) = 6. Six is also the greatest common dimension of all possible array models for 12 and 18 (See Figure 7.3).
Figure 7.3: Modeling the Meaning of Greatest Common Factor Prime Factorization The process of decomposing composite numbers into factors begun in Figure 7.3 may be extended until every factor is a prime number. For instance, the expression 2 x 6 = 12 may be further factored to yield 2 x 2 x 3 = 12. Similarly, the expression 3 x 6 = 18 may be re-written as 2 x 3 x 3 = 18. Both representations, 2 x 2 x 3 = 12 and 2 x 3 x 3 = 18, are called prime factorizations. Mathematicians have long known that there is only one prime factorization for every whole number. In other words, regardless of how one begins to factor a whole number (e.g., 18 = 3 x 6 or 2 x 9), the end result of this process, the prime factorization, is always the same (e.g., 18 = 2 x 3 x 3). Finding the prime factorization for a given whole number n may be approached either systematically or opportunistically. Example 7.3 demonstrates both approaches. By convention, the factors in the prime factorization are listed smallest-to-largest from left-to-right. For instance, the factors in the prime factorization of 18 are listed as 2x3x3, or 2 x 32. Example 7.3 Find the prime factorization for 360. Solution 7.3
The process of prime factorization may be used to determine the greatest common factor of two numbers. The advantage in using this approach is that it takes the guesswork out of the search for the GCF. Example 7.4 illustrates this process. Note that the common factors are underlined for emphasis. Example 7.4 Find GCF(24, 60) Solution 7.4 Prime factorization for 24: 2 x 2 x 2 x 3 Prime factorization for 60: 2 x 2 x 3 x 5 Factors present in both factorizations: 2 x 2 x 3 GCF(24,60) = 2 x 2 x 3 = 12 Least Common Multiple Another topic included in most elementary mathematics textbooks is least common multiple. The least common multiple of 12 and 18, written LCM(12,18), is the smallest whole number having both 12 and 18 as factors. Consequently, LCM(12,18) is divisible by both 12 and 18. Clearly, a common multiple of 12 and 18 is 12 x 18 = 216. Is 216 the smallest common multiple of 12 and 18? No, because 72 = 6 x 12 and 72 = 4 x 18. Is 72 the smallest common multiple? No, again. There is an even smaller common multiple of both 12 and 18, the number 36. A systematic approach to finding the least common multiple for 12 and 18 begins by writing the prime factorizations for each number. Note that the prime numbers common to both factorizations are underlined. Prime factorization for 12: 2 x 2
x 3 Prime factorization for 18: 2 x 3 x 3 In addition to the shared factors, each factorization includes an additional factor not present in the other factorization. Since any common multiple of 12 and 18 must, at a minimum, include all of the factors of both 12 and 18, we can construct the least common multiple of 12 and 18 from these factors, avoiding unnecessary repetitions. In this case, the least common multiple of 12 and 18 may be written as 2 x 2 x 3 x 3 = 36. So, LCM(12,36) = 36. Example 7.5 Find GCF(24, 60) Solution 7.5 Prime factorization for 24: 2 x 2 x 2 x 3 Prime factorization for 60: 2 x 2 x 3 x 5 LCM(24,60) = 2 x 2 x 2 x 3 x 5 = 120
|
||||||
|
|