Number & Operations for Teachers 

Copyright David & Cynthia Thomas, 2009

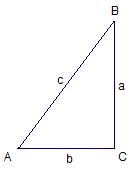
Pythagorean Triples

Among the many mathematical formulas discovered by the ancient Greeks, perhaps the best known is the Pythagorean Theorem: Given a right triangle with hypotenuse of length c and sides of length a and b, c² = a² + b² (See Figure 7.4).

Figure 7.4: Pythagorean Theorem

In many elementary mathematics textbooks, this theorem is used as a context for introducing squares and square roots. In general, introductions of this sort focus on Pythagorean Triples, sets of whole numbers {a, b, c} for which c² = a² + b². Some examples of Pythagorean Triples are {3,4,5}, {8,6,10}, {5,12,13}, {8,15,17}, {12,16,20}, and {7,24,25}. While sets of Pythagorean Triples may be discovered using train-and-error, most teachers prefer a more direct approach when making up sample problems or homework assignments. The following procedure is capable of generating every Pythagorean Triple.

Step 1: Let m and n be integers such that n > m

Step 2: Let a = n² - m²

Step 3: Let b = 2nm

Step 4: Let c = n² + m²

Step 5: Then the set {a,b,c} forms a Pythagorean Triple

A proof that this procedure always generates Pythagorean Triples is straightforward.

a^2 + b^2 =	Left member of the Pythagorean relationship
(n^2 - m^2)^2 + (2nm)^2 =	Substitute (n^2 - m^2) for a and (2nm) for b
(n^4 - 2n^2m^2 + m^4) + (4 n^2m^2) =	Square (n^2 - m^2) and (2nm)
n^4 + 2n^2m^2 + m^4 =	Combine like terms
(n^2 + m^2)^2 =	Factor as (n^2 - m^2) (n^2 - m^2) = (n^2 + m^2)^2
c^2	Since (n^2 + m^2) = c, (n^2 + m^2)^2 = c^2

Example 7.6

Starting with m = 2 and n = 3, create a Pythagorean Triple

Solution 7.6

a^2 + b^2 =	Left member of the Pythagorean relationship
(n^2 - m^2)^2 + (2nm)^2 =	(3^2 - 2^2)^2 + (2x3x2)^2
(n^4 - 2n^2m^2 + m^4) + (4 n^2m^2) =	(5)^2 + (12)^2
n^4 + 2n^2m^2 + m^4 =	25 + 144
(n^2 + m^2)^2 =	169
c^2 =	13^2
c =	13

So, the Pythagorean Triple is {5, 12, 13}

An interesting feature of every Pythagorean Triple {a,b,c} is that either a, b, or c must be a multiple of three. Can you identify another, similar property of Pythagorean Triples? [Hint: Examine a list of Pythagorean Triples.] How might information of this sort help teachers to quickly decide that a given set of whole numbers could not form a Pythagorean Triple?

Tech Resources	Investigate the Pythagorean Theorem at the National Library of Virtual Manipulatives for Interactive Mathematics
	http://matti.usu.edu/nlvm/nav/topic_t_1.html