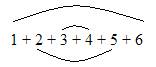|
Number & Operations for Teachers Copyright David & Cynthia Thomas, 2009 |
||||||||||||||||||||||||||||||||
|
Arithmetic Series When the terms of an arithmetic sequence are summed, the result is an arithmetic series. For example, the arithmetic sequence 1, 2, 3, 4, 5 is the basis for the arithmetic series 1 + 2 + 3 + 4 + 5. In terms of the staircase model seen in Figure 7.5, the expression 1 + 2 + 3 + 4 + 5 could be thought of as representing the total number of blocks in a staircase with 5 steps. Similarly, the expression 1 + 2 + 3 + … + 98 + 99 + 100 could be thought of as representing the total number of blocks in a staircase with 100 steps. While this expression could be evaluated by summing all of the terms, the geometric model in Figure 7.7 suggests another method.
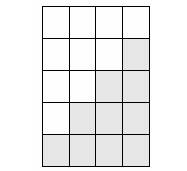
Figure 7.7: Finding the Sum of an Arithmetic Series Figure 7.7 shows a staircase model with 4 steps joined to an identical, though inverted, copy of itself. Note the way the staircases fit together to form the rectangle. The rectangle has one more row than columns. This is always the case, regardless of the number of steps in the staircase. For a four step staircase, the two staircases create a 5 x 4 rectangle composed of 20 blocks. Intuitively, the original staircase must consist of half this amount, or 20 ¸ 2 = 10 blocks. In a related approach, cells are grouped in pairs having equal sums. For instance, the terms in the arithmetic series 1 + 2 + 3 + 4 + 5 + 6 may be grouped as
This pattern was “discovered” in the late 18th century by Carl Friedrich Gauss, age seven. Assigned the task of summing the integers from 1 to 100, Gauss immediately noticed that the sum of the first and last terms of the arithmetic series 1 + 2 + 3 + … + 98 + 99 + 100 is 101, the same sum as all other pairs formed in a similar manner. Recognizing that 50 such pairs could be formed, he multiplied 50 times 101 to obtain the answer 5050. Gauss’ teacher and assistant, Büttner and Bartels, were suitably astonished. Gauss went on to become one of the giants of mathematics, discovering and publishing new mathematics throughout a long and productive life. In terms of the staircase model, Gauss’ problem could be modeled as a rectangle having 101 rows and 100 columns. Consequently, the rectangle formed would consist of 100 x 101 = 10100 blocks. Half of these, or 5050 blocks, would “belong” to the original staircase. Both approaches suggests the following formula for computing the sum of an arithmetic series having n terms (where n is an even number), the first term is al, and the last term is an: Sum = (n/2)(al + an). Example 7.8 Find the sum of the first 100 odd whole numbers. Solution 7.8
We now apply the same procedure to arithmetic series having an odd number of terms. For instance, the series 1 + 2 + 3 + 4 + 5 has a sum of 15. If we apply the formula for finding the sum of an arithmetic series with an even number of terms to this series, we obtain (n/2)(al + an) = (5/2)(1 + 5) = (2.5)(6) = 15, which is the correct result. To understand why the same formula works for series having either an even or an odd number of terms, consider the geometric model shown in Figure 7.8. Clearly, the shaded area could be computed as Sum = n(n + 1)/2 = 5(6)/2 = 15. Rearranging terms, this formula may also be written as Sum = (n/2)(1 + n), which is the same as the formula for the sum of an arithmetic series with an even number of terms and a first term of 1.
Figure 7.8: Arithmetic Series with an Odd Number of Terms |
||||||||||||||||||||||||||||||||
|
|