|
Number & Operations for Teachers Copyright David & Cynthia Thomas, 2009 |
|||||||||||||||||||||||||||||||||||||
|
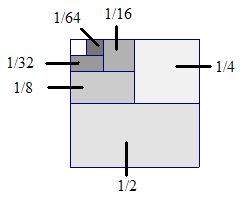
Geometric Series If the terms of the geometric sequence Figure 7.9 models
the terms of this series as regions in a unit square. Geometrically, the sum of this series
corresponds to the shaded area in the figure.
Since all but 1/64th of the unit square is shaded, the sum
of the series must equal 1 – 1/64 = 63/64.
The same result could be obtained by adding the terms in the series
Figure 7.9:
Geometric Series Infinite Geometric
Series If a geometric series has an infinite number of terms, its
sum may or may not be finite. For
instance, it is clear that the sum of the infinite geometric series 2 + 4 + 8
+ 16 + 32 + 64 + … must be infinite, because each term makes the sum
significantly larger. On the other
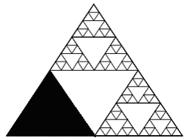
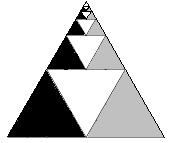
hand, Figure 7.9 suggests that the sum of the infinite series What determines whether the sum of a geometric series is finite or infinite? The common ratio between successive terms. In general, if the common ratio between successive terms is greater than one, each term is larger than the previous term, so the sum of the series grows without bound. On the other hand, if the absolute value of the common ratio between successive terms is less than one, each term is smaller than the previous term, so the sum of the geometric series is bounded and is therefore finite. The object seen in Figure 7.10 is meant to approximate the Sierpinski triangle. Because the Sierpinski triangle contains an infinite number of nested equilateral triangles, it can never be completely drawn, but it can be imagined. The object in Figure 7.10 is meant to engage your imagination. Construction of the Sierpinski triangle begins with an equilateral triangle. The midpoints of each side are connected, dividing the original triangle into four equilateral triangles, each having 1/4th the area of the original triangle. The same procedure is then repeated on those triangles and on subsequent triangles created by this process. In Figure 7.10 a series of these triangles is shaded black. Your task is to represent that portion as a geometric series to express its area as a fraction of the original equilateral triangle.
Figure 7.10: Partitioning the Sierpinski Triangle If the original equilateral triangle has area 1, the first
partitioning creates four smaller equilateral triangles, each with area ¼
that of the original. When each of
those triangles is partitioned, even smaller equilateral triangles are
created, each with area 1/4th of 1/4th, or (1/4)2. The next partitioning creates equilateral
triangles with area 1/4th of 1/4th of 1/4th,
or (1/4)3. And
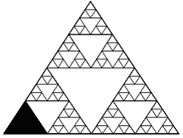
so on. The last object in Figure 7.10
suggests that the triangular areas along the left edge of a fully developed
Sierpinski triangle could be represented using the geometric series you that those triangles constitute 1/3 the area of the original triangle.
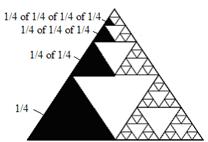
Figure 7.11: Seeing the Area of the Black Region That being the case, we may represent the shaded area
using the infinite geometric series This sum may also be modeled using a spreadsheet. Table 7.2 shows the value of each term expressed as a decimal and the accumulating value of the sum as subsequent terms are added. Clearly, this series approaches 1/3 as more and more terms are added.
Table 7.2:
Numerical Model for the Geometric Series |
|||||||||||||||||||||||||||||||||||||
|
|