Concepts and Connections

Shape

Necessary Conditions--Concepts & Connections

In the directed activities Segment Length and Angle Sums you investigated constraints on the segments and angles used to create triangles. Concerning segments, the most fundamental constraint is known as the Triangle Inequality Theorem. This theorem states that “The sum of the measures of any two sides of any triangle must be greater than the measure of the third side.” This theorem was demonstrated using three lengths of dry spaghetti in the Segment Length directed activity. As illustrated in Figure 1.4, segments a, b and c cannot be jointed to create a triangle because the combined lengths of segments a and b is insufficient to span segment c.

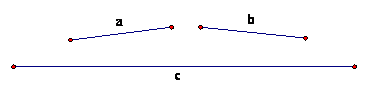
Figure 1.4: Triangle Inequality Theorem

Concerning angles, the paper folding activity in the directed activity Angle Sums demonstrates that “The sum of the measures of the angles of every triangle is 180°”. Because this demonstration does not explicitly deal with all possible triangles, it does not constitute a formal mathematical proof. On the other hand, it does provide a compelling basis for belief in and a convenient context for discussing the meaning of the theorem. The introduction to this chapter asks, “Given a particular set of segments and/or angles, is it always possible to construct a triangle?” Based on the findings of Segment Length and Angle Sums, it is clear that the answer to this question is no.

In the directed activity Construct an Equilateral Triangle Using Straightedge-and-Compass,

you are asked to construct an equilateral triangle using straightedge-and-compass. One version of that construction appears in Table 1.1 and is illustrated in Figure 1.5.

Step	Action
1	Draw segment AB.
2	Place the point of the compass at A. Using segment AB as a radius, draw circle A.
3	Place the point of the compass at B. Using segment BA as a radius, draw circle B.
4	Mark the intersections of circle A and circle B and label them C and D.
5	Draw segments AC and BC.
6	ΔABC is equilateral

Table 1.1: Construction of an Equilateral Triangle Using Straightedge-and-compass

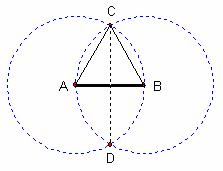
Figure 1.5: Construction of an Equilateral Triangle Using Straightedge-and-compass

The algorithm listed in Table 1.1 constitutes a sort of recipe for constructing an equilateral triangle. As with most recipes, there is no explanation of why the algorithm works. In Euclidean geometry, justification takes the form of logical arguments. Notice the manner in which the following statements support the steps in the construction by referring to Euclidean definitions, postulates, and common notions about equality:

· Because a circle may be drawn with any center and radius (Postulate 3), circle A and circle B may be drawn with identical radii.

· Because a segment may be drawn between any two points, segments AC and BC may be drawn.

· Segment AC is a radius of circle A and segment BC is a radius of circle B (Definition of a radius).

· Because all radii of a given circle are equal in length (Definition of a circle), radii AC and AB of circle A are equal in length and radii BA and BC of circle B are equal in length.

· Since AC = AB and AB = BC, AC = AB = BC (Transitive Property of Equality).

· Therefore ΔABC is equilateral (Definition of Equilateral).

Logical arguments of this sort need not employ a particular format. What is required is a systematic argument in which all actions and conclusions are justified with references to definitions, postulates, and other accepted notions and/or theorems. Learning to construct, evaluate, and appreciate logical arguments is a priority of the NCTM Reasoning & Proof Standard, which states, “Instructional programs from pre-kindergarten through grade 12 should enable all students to

v Recognize reasoning and proof as fundamental aspects of mathematics;

v Make and investigate mathematical conjectures;

v Develop and evaluate mathematical arguments and proofs;

v Select and use various types of reasoning and methods of proof.“

This standard cannot be met through the use of occasional reasoning activities. Instead, teachers of mathematics should encourage students to justify their thinking everyday and value their attempts to justify their conclusions.