Shape
Copyright David & Cynthia Thomas, 2009
More Triangle Recipes--Concepts & Connections
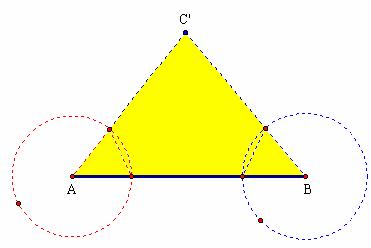
Directed activities Angle-Side-Angle and Angle-Angle-Side focus on two additional strategies for constructing and/or duplicating triangles (See Figure 1.20).

Figure 1.20: Angle-Side-Angle vs. Angle-Angle-Side
In the case of Angle-Side-Angle, given triangle ![]() with known side AB
between known angles
with known side AB
between known angles ![]() and
and
![]() (ASA), the task is to
construct a triangle
(ASA), the task is to
construct a triangle ![]() congruent
to
congruent
to![]() . As a context
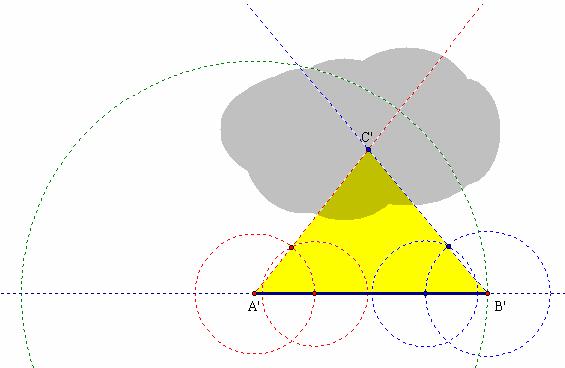
for this question, imagine that the purpose of the construction is to determine
the location (C’) of a buried treasure based on an identical triangle
. As a context
for this question, imagine that the purpose of the construction is to determine
the location (C’) of a buried treasure based on an identical triangle ![]() at another
location. The strategy is to construct
at another
location. The strategy is to construct ![]() identical to
identical to ![]() and identify the
location of C’ in the gray region of Figure 1.21. The steps in the
construction are presented in Table 1.6. Using The Geometers
Sketchpad (See 1_ASA.gsp), students may
verify this result directly by measuring the sides and angles and that the
treasure is buried at point C’.
and identify the
location of C’ in the gray region of Figure 1.21. The steps in the
construction are presented in Table 1.6. Using The Geometers
Sketchpad (See 1_ASA.gsp), students may
verify this result directly by measuring the sides and angles and that the
treasure is buried at point C’.
|
Step 1 |
A random point A’ is plotted on a working line. |
|
Step 2 |
Using A’ as the center and segment AB in |
|
Step 3 |
Using the angle copying strategy demonstrated in Table 1.5, a ray is constructed with endpoint A’. |
|
Step 4 |
Using the angle copying strategy demonstrated in Table 1.5, a ray is constructed with endpoint B’. |
|
Step 5 |
The intersection of these two rays is labeled point
C’,creating |
Table 1.6: Angle-Side-Angle Construction
|
|
|
|
Figure 1.21: Angle-Side-Angle
In the case of Angle-Angle-Side, given triangle ![]() with known angles
with known angles ![]() and
and ![]() , and with known side BC
(AAS), the task is to construct a triangle
, and with known side BC
(AAS), the task is to construct a triangle ![]() congruent
to
congruent
to![]() ? As a context for
this question, imagine that a surveyor forgets to record the location of point
A on a map. He does recall that, seen from point A, there is an angle
? As a context for
this question, imagine that a surveyor forgets to record the location of point
A on a map. He does recall that, seen from point A, there is an angle ![]() between telephone
poles at locations B and C. He also recalls that, seen from point B,
there is and angle
between telephone
poles at locations B and C. He also recalls that, seen from point B,
there is and angle![]() between
point A and C. Finally, he knows the distance from B to C.
The strategy is to construct
between
point A and C. Finally, he knows the distance from B to C.
The strategy is to construct ![]() congruent
to
congruent
to ![]() and to identify the
location of A’ in Figure 1.22. The steps in the construction are
presented in Table 1.7. Using The Geometers Sketchpad (See 1_AAS.gsp), students may verify this result directly
by measuring the angles.
and to identify the
location of A’ in Figure 1.22. The steps in the construction are
presented in Table 1.7. Using The Geometers Sketchpad (See 1_AAS.gsp), students may verify this result directly
by measuring the angles.
|
Step 1 |
A random point B’ is plotted on a working line. |
|
Step 2 |
Using B’ as the center and segment BC in |
|
Step 3 |
Using the angle copying strategy demonstrated in Table
1.5, |
|
Step 4 |
Using the angle copying strategy demonstrated in Table
1.5, |
|
Step 5 |
Using the Sketchpad’s construction tools, a segment
parallel to ray PQ containing point C’ is drawn, creating |
Table 1.7: Angle-Angle-Side
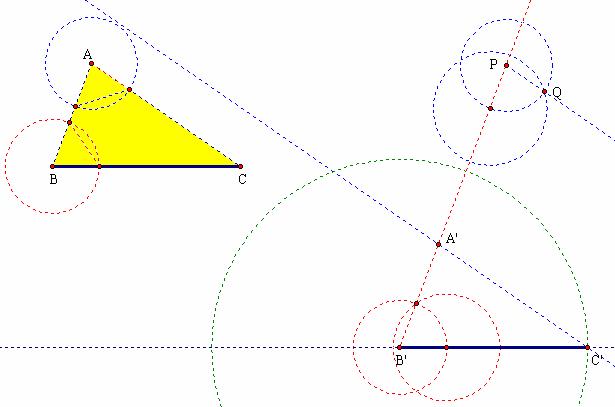
Figure 1.22: Angle-Angle-Side
A somewhat different situation is encountered in directed activities Angle-Angle-Angle and Side-Side-Angle. In both of these activities, a task is posed for which the given information is insufficient to specify a unique triangle. For instance, given three angles with a sum of 180°, infinitely many triangles are possible, two of which are seen in Figure 1.23. That being the case, there is no way to know which triangle is the intended result.
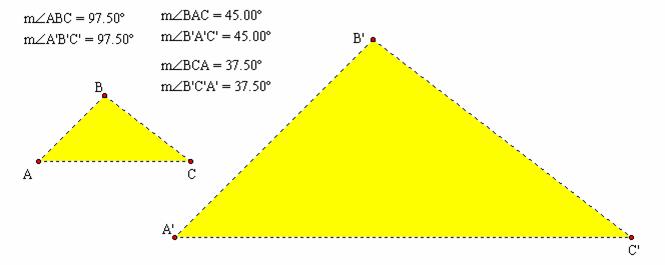
Figure 1.23: Angle-Angle-Angle
A different situation is encountered in directed activity Side-Side-Angle (See Figure 1.24). Given two sides and a non-included angle (e.g., CB, BA, and ÐCBA), two different triangles may be possible (e.g., !CBA and !DBA). These findings provide a basis for answering the fourth and final question asked in the introduction to Chapter One, “Is it ever possible to construct more than one triangle from a given set of segments and/or angles?” The answer is yes.

Figure 1.24: Side-Side-Angle