Concepts and Connections

Shape

Area of Triangles--Concepts & Connections

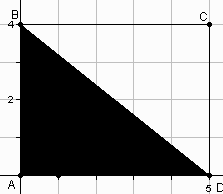
Figure 2.4 shows two objects which, while related, are not identical. The object on the left is a square. Every square consists of four line segments of equal length joined at their endpoints to form right angles. The square itself is a one-dimensional path, the length of which is called the perimeter of the square. By contrast, the interior of the square is a two- dimensional region, the measure of which is called the area of the square. By convention, statements such as “Find the area of the square” are understood to mean “Find the area of the interior of the square” or “Find the area enclosed by the square.”

Figure 2.4: A Square and its Interior

If the length of each side of a square is 1 unit, then the perimeter of the square is 4 units. Squares with these properties are called unit squares. By convention, unit squares are said to have an area of 1 square unit (i.e., 1 unit²).

Figure 2.5: Areas of Rectangles

Figure 2.5 presents a 2x4 array of unit squares, the interior of the array, and a composite view of both the array and its interior. By counting the square units in the composite view, an area of eight square units is obtained for the array. It should also be visualized as two rows with four squares in each row or four columns with two squares in each column. However area of a rectangle is usually thought of as the product of a multiplication. This is obtained by multiplying the dimensions of the array, 2 rows with 4 squares in each row would be written as 2´4= 8 square units or 4 columns with 2 squares in each column would be written as 4´2= 8 square units. The conventional formula is A=length x width but may also be written as A=bh. Similarly, the perimeter of the array may be counted as 12 units or computed as 2·4+2·2 = 12 units. The conventional formula for determining perimeter of a rectangle is P= 2l+2w or P=2b+2h.

Using understanding of area of a rectangle as a basis, the area of triangles is also easily visualized and understood. For instance, in Figure 2.6, since is a diagonal of rectangle ABCD, ΔABC is clearly one-half of rectangle ABCD. Therefore, the area of ΔABC must be half the area of ABCD.

Figure 2.6: Area of a Right Triangle

In order to compute the area of any triangle, you need detailed information about the triangle’s sides and/or other features. In some situations, that information may be provided by contextual clues, as in the case of lattice triangles. Lattice Triangles investigates the area of triangles for which each vertex has integer coordinates relative to a rectangular coordinate system. In Figure 2.7, ΔABC is divided into two adjacent triangles, ΔADC and ΔBDC. Each of these triangles may be seen as have of a rectangle. Intuitively, ΔADC has half of the area of rectangle ADCE. Since the rectangle has a countable area of 4 square units, the area of ΔADC is 2 square units. Using similar reasoning on rectangle BDCF, the area of ΔBDC is 6 square units. Combining these findings, the area of ΔABC is 8 square units. Note that this is also half of rectangle ABFE. This is an additive approach to computing the area of the triangle.

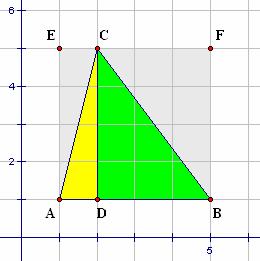
Figure 2.7: Lattice Triangles & the Additive Approach

In Figure 2.8, a subtractive approach is used to compute the area of ΔABC. As a first step, the area of rectangle FEDA is determined to be 15 square units by counting unit squares. The areas of ΔAFC, ΔADB, and ΔBCE are then subtracted to obtain the area of ΔABC. Doing so yields 15 – 5 – 3 – 1.5 = 15 – 9.5 = 5.5 square units.

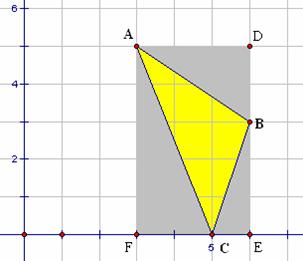
Figure 2.8: Lattice Triangles & the Subtractive Approach

A more common and versatile approach to finding the area of a triangle is to use an algebraic formula. The directed activity Area Formulas examines the basis for and use of the triangle area formula , where b = one side of the triangle and h = the altitude to that side from the opposite vertex (i.e., the height). In Figure 2.9, the altitude to side AC of ΔABC is shown as segment BD.

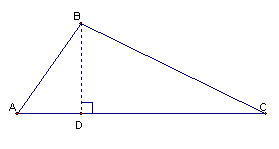
Figure 2.9: Altitude of a Triangle

Three other interior lines are illustrated in Figure 2.10.

· Perpendicular bisector. Line EF is constructed perpendicular to side BC at point E, the midpoint of side BC.

· Angle bisector. Ray AD bisects , intersecting side BC at point D.

· Median. Segment AE vertex A to the midpoint of the opposite side, point E.

Figure 2.10: Interior Lines

Figures 2.11 and 2.12 illustrate the role of the altitude in triangle area computations. As illustrated in Figure 2.11, the height (i.e., the altitude) of right triangle ΔABC relative to side BC is determined by the perpendicular distance from point A to point B. Intuitively, the area of ΔABC is half that of rectangle ABCD. Since the area of a rectangle is given by the formula A = bh, or AB*BC, the formula for the area of ΔABC is given by , or (1/2)*AB*BC.

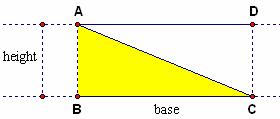
Figure 2.12 applies similar logic to acute triangle ΔABC. In this case, the height of the triangle relative to side BC is determined by the perpendicular distance from point E to point B. Intuitively, the area of ΔABC is half that of parallelogram ABCD. As shown in Figure 2.12, the area of this parallelogram is equivalent to that of rectangle EBCF. Since the area of this rectangle is given by the formula A = bh, or EB*BC, the formula for the area of ΔABC is given by , or (1/2)*EB*BC.

Figure 2.11: Right Triangle Area

Figure 2.12: Acute Triangle Area