Shape
Copyright David & Cynthia Thomas, 2009
Sides, Angles, Interior Lines & Points--Concepts & Connections
The directed activity Pythagorean Theorem focuses on an ancient relationship now known as the Pythagorean Theorem. Pythagoras (569 – 475 BC) lived in a Greek community in southern Italy and founded a quasi-religious “brotherhood” credited with many discoveries, including the relationship illustrated in Figure 2.20. In modern notation, c2 = a2 + b2.
In a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.

Figure 2.20: Pythagorean Theorem
In practice, the Pythagorean Theorem is used for two different but related purposes:
1. Given a right
triangle, to compute the length of one side given the measures of the other two
sides. Used in this manner, the theorem may be stated, “If a triangle is
a right triangle, then c2 = a2 + b2.”
For example, in a given right triangle, if a = 6 and b = 8, then a2
+ b2 = 62 + 82 = 36 + 64 = 100.
Since c2 = 100, c = ![]() .
Alternatively, in a given right triangle, if c = 10 and a =
6, then c2 – a2 = b2, so
102 – 62 = 100 – 36 = 64 = 82. Consequently,
b = 8.
.
Alternatively, in a given right triangle, if c = 10 and a =
6, then c2 – a2 = b2, so
102 – 62 = 100 – 36 = 64 = 82. Consequently,
b = 8.
2. Given three sides of a triangle, to determine whether the triangle is a right triangle. Used in this manner, the theorem may be stated, “If c2 = a2 + b2, then the triangle is a right triangle.” For example, in a given triangle, if c = 10, a = 6, and b = 8, then a2 + b2 = 62 + 82 = 36 + 64 = 100 = 102 = c2. So, the given triangle is a right triangle.
The directed activity Pythagorean Triples deals with a related topic. A Pythagorean Triple is a set of three positive integers that satisfy the Pythagorean relationship, c2 = a2 + b2. Common textbook examples include the sets {3,4,5} and {5,12,13}. These sets correspond to triangles with sides of length 3-4-5 and 5-12-13. Any set of integers that is a multiple of these sets is also a Pythagorean Triple. For example, the sets {6,8,10} and {10,24,26} are Pythagorean Triples.
As a teacher of mathematics, you will probably plan and deliver lessons involving right triangles. Knowing how to generate sets of Pythagorean Triples will make this taks easier and the lessons richer than they might be otherwise. The following algorithm provides such a method. Given any pair of positive integers {m,n} such that m > n, a Pythagorean Triple may be computed as the the set {m2 – n2, 2mn, m2 + n2}. For example, if m = 5 and n = 4,
m2 – n2 = 52 – 42 = 9
2mn = 2(5)(4) = 40
m2 + n2 = 52 + 42 = 41
Therefore 9, 40, and 41 are Pythagorean Triples
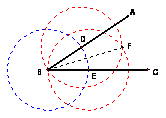
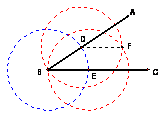
The directed activities Angle bisectors, Perpendicular lines, and Parallel lines deal with three basic Euclidean constructions. Table 2.1 summarizes the steps in each construction.
|
|
Construction |
Steps |
|
Angle Bisector |
GSP Model 2_AngleBis.gsp |
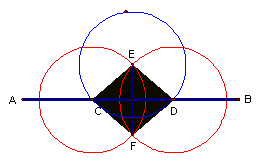
· Using B as the center, draw any circle that intersects BA in point D and BC in point E · Using the same radius, draw two circles with centers D and E · Find F, the intersection of those circles · Draw segment BF · Segment BF bisects ŠABC Note: BDFE is a rhombus. |
|
Perpendicular at Point |
GSP Model 2_PerpAtPt.gsp |
· Draw a circle with center C · Find D and E, the intersections of the circle and line AB · Using D and E as centers and DE as a radius, draw two circles · Find the intersection of the two circles, F and G · Draw segment FG · FG is perpendicular to AB at point C Note: DFEG is a rhombus. |
|
Parallel Segments |
GSP Model 2_ParallelSegs.gsp |
· Using B as the center and BD as the radius, draw a circle that intersects BA in point D and BC in point E · Using the same radius, draw two circles with centers D and E · Find F, the intersection of those circles · Draw segment DF · Segment DF is parallel to BC Note: BDFE is a rhombus. |
Table 2.1: Three Euclidean Constructions
Two of the constructions in Table 2.1 have several features in common. For instance, construction 3 proceeds as construction 1 up to the last step then concludes by drawing segment DF instead of segment BF. In each case, the construction begins as if the goal were to create a rhombus BDFE. This strategy works because …
· All four sides of a rhombus are congruent;
· The diagonals of a rhombus bisect the angles of the rhombus; and
· Opposite sides of a rhombus are parallel.
In construction 1, the rhombus itself is never drawn, but one of its diagonals, BF, is presented as the bisector of ŠABC. Since the diagonals of every rhombus bisect the angles of the rhombus, we may identify BF as the bisector of ŠABC. In construction 3, segment BF is presented as being parallel to line BC. Since the opposite sides of every rhombus are parallel, we may identify segment BF as being parallel to segment BE and line BC.
A similar set of observations may be used to present a unifying perspective on the constructions in Table 2.2. In each case, construction of a rhombus leads directly to the desired result. So, rather than viewing each construction as a lengthy set of steps, one may take a more strategic view: Using the given information, construct a rhombus then interpret the results in terms of the general properties of a rhombus.
|
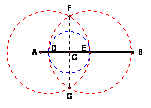
Task: Construct the perpendicular bisector of segment AB
GSP Model 2_PerpBis.gsp
Strategy: Build Circles A and B that have congruent radii. Build rhombus ABCD in which all sides are radii of either Circle A or B and therefore are congruent. Diagonals of a rhombus are perpendicular. |
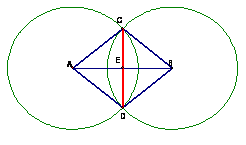
Task: Construct the perpendicular to line or segment AB from a point E not on AB
GSP Model 2_PerpFrPt.gsp Strategy: Construct a circle with center E that intersects segment AB at two points C and D. Using the same radius, construct circles with centers C and D. In rhombus ECFD diagonal EF is perpendicular to diagonal CD. |
Table 2.2: Unifying Perspective
The directed activity Water Treatment Plant asks you to locate a point equidistant from three non-collinear points. Begin by constructing the perpendicular bisectors of the sides of the triangle determined by the three communities (See Figure 2.21). Surprisingly, all three perpendicular bisectors intersect at a common point called the circumcenter. Furthermore, a circle drawn with this point as center and the distance to vertex A as radius also contains vertices B and C. In other words, the circumcenter is equidistant from all three vertices (Why?). This point marks the location of the water treatment plant.
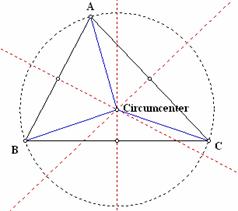
Figure 2.21: Circumcenter of a Triangle
The bisectors of the angles of a triangle intersect at a point called the incenter. This point may be used as the center of a circle that is tangent to the three sides of the triangle (See Figure 2.22). Using the Geometers Sketchpad model 2_Incenter.gsp, examine the construction. What is the significance of this model relative to the directed activity School Bus Garage? Where would you put the school bus garage? Why?
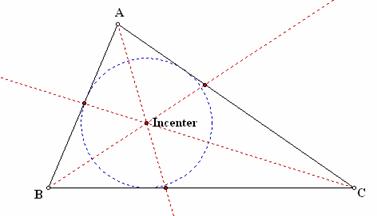
Figure 2.22: Incenter of a Triangle
The directed activity Balance Point asks you to find an interior point of a cut-out triangle on which the entire triangle will balance. Begin by finding the midpoint of each side of the triangle. Next, draw segments called medians from each vertex to the midpoint of the opposite side. As seen in Figure 2.23, the medians of a triangle intersect at a point called the centroid. This point is also called the center of gravity of the triangle, the point where a cut-out version of the triangle would balance on the point of a pin. Use the triangles you cut out in Directed Activity 2.11. Do the triangles balance on the centroid? Be as accurate as possible when finding the midpoint of the sides and drawing the medians.
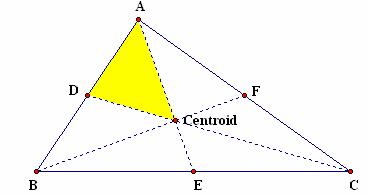
Figure 2.23: Centroid of a Triangle