Concepts and Connections

Shape

Naming, Describing, and Constructing Polygons--Concepts and Connections

Directed Activity Names & Attributes of n-gons. Because geometry creates and uses so many types of objects, a specialized vocabulary has evolved for naming and describing their features. Acquiring and using this vocabulary is an important aspect of geometric learning and communication.

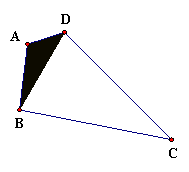
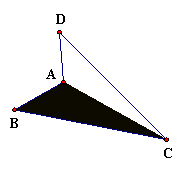
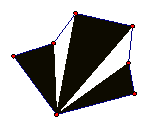
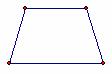
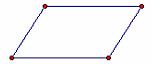
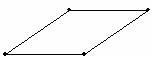
Figure 3.4: Polygons

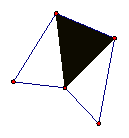
Figure 3.5: Regular Polygons

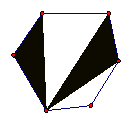
The objects seen in Figure 3.4 are examples of a class of figures called polygons. Every polygon consists of a finite number of segments joined end-to-end to create a closed figure; that is, the resulting figure must have an inside and an outside. Furthermore, the figure must not intersect itself. If, in addition, every segment is the same length, as in Figure 3.5, the polygon is said to be regular. Figure 3.6 presents a family of regular polygons, all of which have the same side length. Can you name each polygon?

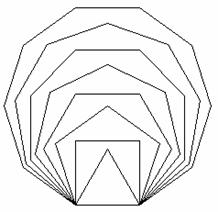
Figure 3.6: Family of Regular Polygons

Asked to name the objects seen in Figure 3.6, one might say triangle, square, pentagon, and 6-gon, respectively. It is worth noting that, even in a list this brief, several naming conventions may be used. In naming the …

· Three sided object a triangle, information about the object is encoded in its name.

o The prefix tri-, indicates the quantity 3;

o The root word -angle, refers to the object’s vertices;

· Four sided object a square, no information is encoded in its name.

· Five sided object a pentagon, information about the object is encoded in its name.

o The prefix penta-, indicates the quantity 5;

o The root word –gon refers to the object’s sides

· Six sided object a 6-gon, information about the object is encoded in its name.

o The prefix 6- indicates the quantity without using a specialized counting vocabulary;

o The root word –gon refers to the object’s sides.

Using the last of these approaches, a polygon with 13 sides is called a 13-gon, a polygon with 99 sides is called a 99-gon, and a polygon with an arbitrary number of sides is called an n-gon. Because of its clarity and simplicity, this system is preferred by contemporary mathematicians. At the same time, all students of mathematics need to be familiar with traditional naming conventions for polygons with 10 or fewer sides, as these names occur frequently in both mathematical and normal discourse. These alternative names are presented in Table 3.1.

Number of Sides	Traditional Name	Contemporary Name
3	Triangle	3-gon
4	Quadrilateral	4-gon
5	Pentagon	5-gon
6	Hexagon	6-gon
7	Septagon	7-gon
8	Octagon	8-gon
9	Nonogon	9-gon
10	Decagon	10-gon

Table 3.1: Polygon Naming Alternatives

Because quadrilaterals are used extensively in mathematics and its applications, a specialized vocabulary has evolved that differentiates 4-sided figures based on their angles and sides.

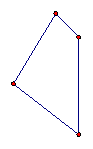
· Interior Angles. Every quadrilateral has four sides and four angles. As suggested by Figures 3.7 and 3.8, every quadrilateral also has an angle sum equal to that of two triangles, or 360°. In convex quadrilaterals, both diagonals (e.g., AC and BD) lie within the interior of the quadrilateral. In a concave quadrilateral, one diagonal (e.g., BD) lies outside of the quadrilateral and one diagonal (e.g., AC) lies inside the quadrilateral.

Figure 3.7: Convex Quadrilateral		Figure 3.8: Concave Quadrilateral

N = 5 # Interior Triangles = 3 3 * 180° = 540° Measured Angle Sum = 540°	N = 6 # Interior Triangles = 4 4 * 180° = 720° Measured Angle Sum = 720°		N = 7 # Interior Triangles = 5 5 * 180° = 900° Measured Angle Sum = 900°

Table 3.2: Polygon Angle Sums

A similar approach may be used to determine the sum of the interior angles of any n-gon. Note that the number of interior triangles in each polygon in Table 3.2 is two less than the number of sides. Since every triangle has an angle sum of 180°, the interior angle sum may be written as (n - 2)(180°). If a polygon is regular, every interior angle is identical (See Figure 3.9). Consequently, each interior angle has the same measure, (Why?).

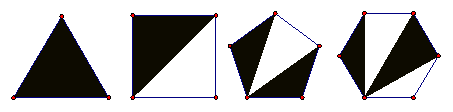
Figure 3.9: Interior Angle Sums for Regular Polygons

Example 3.1

Find the measure of an interior angle of a regular 10-gon.

Solution 3.1

· Exterior Angles. Angles formed by one side of the triangle and an extension of an adjacent side are called exterior angles. As seen in Figure 3.10, exterior angles A, B, and C lie outside of ΔABC. Using Geometers Sketchpad model 3_ExteriorAngleSum.gsp, you may vary the positions of vertices A, B, and C. In every case, the exterior angles will have the same sum, 360°. Clicking the Zoom button will shrink the triangle to a point. In the process, the vertices of the arc sectors representing the exterior angles will also converge to a common point, showing that the three arc sectors may be assembled to create a filled-in circle. Geometrically, how does this support the idea that the sum of the exterior angles is 360°?

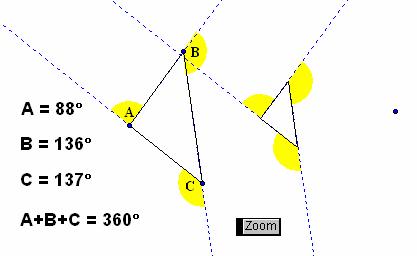
Figure 3.10: External Angle Sum

Alternatively, we may use algebraic thinking to obtain the same result.

- The sum of the interior angles of every triangle is 180°; (Why?)

- The sum of each interior angle and its exterior angle is also 180°; (Why?)

- The sum of all three pairs of interior and exterior angles is 540°; (Why?)

- The sum of the exterior angles is therefore 360°. (Why?)

- Use similar thinking to explore the exterior angle sums of 4-gons, 5-gons, n-gons.

· Central Angles. If a polygon is regular, it may be inscribed in a circle. The center of that circle also serves as the center of the polygon. For instance, in Figure 3.11, point P is the center of regular polygon ABCDE. Segments connect each vertex to point P. Each of the central angles formed in this manner has a measure of 360°/5 = 72° (Why?). Compare this value to that of ÐXBC, the external angle at vertex B. Are they the same or different? Why? Use similar reason to compare the central and external angles of regular 4-gons, 6-gons, etc. What do you notice?

Figure 3.11: Exterior vs. Central Angles

· Sides. The perimeter of every polygon is computed as the sum of its side lengths.

Tables 3.3 and 3.4 illustrate a number of quadrilaterals and organize them according to the properties of their sides and angles. Note: Three of the cells of the table are blank. Explain why quadrilaterals with the indicated features cannot exist.

Sides	No congruent sides	1 pair of congruent sides	2 pair of congruent sides
No parallel sides			Kite
1 pair of parallel sides	Trapezoid	Isosceles trapezoid
2 pair of parallel sides			Parallelograms (See Table 3.5)

Table 3.3: Quadrilateral Names

Consecutive sides may be different lengths

Consecutive sides must be the same length

Consecutive

angles must be supplementary

Parallelogram

Rhombus

Each angle must be 90°

Rectangle

Square

Table 3.4: Parallelogram Names

On the basis of the information presented in Table 3.4, one may make the following statements. Explain the basis for each statement.

· A rhombus is a parallelogram in which the all sides are the same length.

· A square is a rhombus in which all angles are the same measure.

· Every square is both a rhombus and a rectangle.

The tree diagram in Figure 3.12 provides an overview of quadrilateral relationships.

Figure 3.12: Quadrilateral Relationships

Directed Activity Constructing a Square. The postulates for paper folding may be used to construct a wide variety of geometric figures. For instance, the folds used to create square CEGE’ in Figure 3.13 are listed in Table 3.5.

Step 1	Line AB is folded across the sheet and a point C selected as a vertex of the square.
Step 2	Line AB is folded on itself at point C, producing a line CD perpendicular to AB at C.
Step 3	Line AB is folded on itself at point E, producing a line EF perpendicular to AB at E.
Step 3	Line CD is folded on line CB. Consequently line CH intersects line EF at point G.
Step 4	Line EF is folded on itself point G, producing a line GE’ perpendicular to EF at point G.
Step 5	Points C, E, G, and E’ are the vertices of a square.

Table 3.5: Folding a Square

At what point in this process is the size of the square determined? Why does this construction “work”? Practice this construction until you can perform it reliably. Then experiment with a Geometers’ Sketchpad version of this construction, 3_FoldSquare.gsp.

Figure 3.13: Folding a Square

Directed Activity Constructing a Parallelogram. The folds used to create parallelogram PQRS in Figure 3.14 are listed in Table 3.6.

Step 1	Line l is folded on itself at an arbitrary point L, producing a line n perpendicular to l.
Step 2	Line n is folded on itself at an arbitrary point L’, producing a line l’ parallel to l.
Step 3	Line m is folded on itself at an arbitrary point M, producing a line o perpendicular to m.
Step 4	Line o is folded on itself at an arbitrary point M’, producing a line m’ parallel to m.
Step 5	Lines l, m, l’, and m’ intersect in points P, Q, R, and S, the vertices of a parallelogram.

Table 3.6: Folding a Parallelogram

What purpose do points L and M serve in this construction? Why does this construction “work”? Practice this construction until you can perform it reliably. You may experiment with a Geometers Sketchpad model of this construction, 3_Parallelogram.gsp.

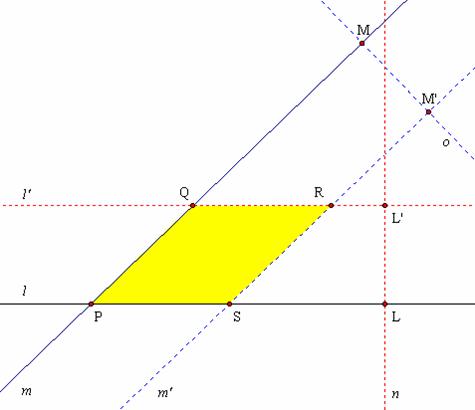
Figure 3.14: Folding a Parallelogram