Concepts and Connections

Shape

Perimeter & Area of Polygons--Concepts and Connections

Challenge: The Meaning of Area.. If you compare your cell counts and area estimates to those of other students, you will see that the data differ, depending on how the transparencies were positioned relative to the objects. Your general findings, on the other hand, should be the same:

· Counting only cells that are entirely contained within each object, you should have obtained progressively better estimates as the grid cells became smaller. This finding suggests that better estimates could be obtained by using smaller and smaller cell grids. It also suggests that this approach systematically underestimates the area of each object.

· Counting all cells that are entirely or partially contained within object, everyone should have obtained progressively better estimates as the grid cells became smaller. This finding also suggests that better estimates could be obtained by using smaller and smaller cell grids. It also suggests that this approach systematically overestimates the area of each object.

Directed Activity Lattice Polygons. In order to compute the area of any polygon, you need detailed information about the object’s sides and/or angles. In some situations, that information may be provided by contextual clues, as in the case of lattice polygons. Directed Activity Lattice Polygons investigates the area of polygons for which each vertex has integer coordinates relative to a rectangular coordinate system. In Figure 3.23, a lattice polygon is divided into adjacent triangles and rectangles. Intuitively, the area of the polygon is equal to the sum of the areas of these regions. Beginning with the 2x2 square and proceeding clockwise around the object, the sum of these areas may be computed as 4 + 1 + 1.5 + 0.5 + 1 = 8 units². This is an additive approach to computing the area of the polygon.

Figure 3.23: Lattice Polygon & the Additive Approach

In Figure 3.24, a subtractive approach is used to compute the area of the polygon. As a first step, the area of rectangle PQRS is determined to be 16 square units by counting unit squares. The areas of ΔAPD, ΔDQC, ΔCRB, and ΔBSA are then subtracted to obtain the area of polygon ABCD. Doing so yields the expression 16 – 3 – 1.5 – 1.5 - 1 = 16 – 7 = 9 units².

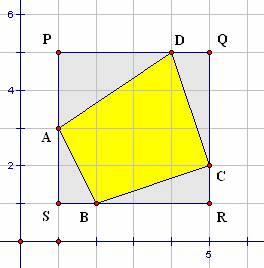
Figure 3.24: Lattice Triangles & the Subtractive Approach

Directed Activity Perimeter vs. Area of Rectangles. Figure 3.25 shows a Geometers Sketchpad model 3_MaxRectangle.gsp of a rectangle. Note that the area is given in terms of square centimeters, while the perimeter is given in terms of centimeters. The perimeter of the rectangle may be changed by dragging the point labeled Perimeter. The relative lengths of the sides may be changed by dragging the point labeled Relative Length. Experiment with this model and answer the question, For any given perimeter, what shape rectangle has the greatest area?

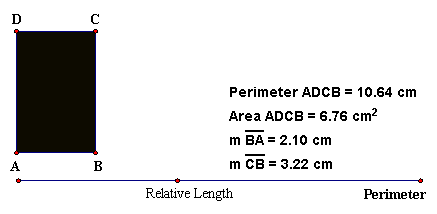
Figure 3.25: Maximum Area for a Rectangle with Fixed Perimeter

Directed Activity Perimeter vs. Area of Parallelograms. Figure 3.26 shows a Geometers Sketchpad model 3_MaxParallelogram.gsp of a parallelogram. The perimeter of the parallelogram may be changed by dragging the point labeled Perimeter. The relative lengths of the sides may be changed by dragging the point labeled Relative Length. And the “lean” of the parallelogram may be changed by moving the Drag Point. Experiment with this model and answer the question, For any given perimeter, what shape parallelogram has the greatest area?

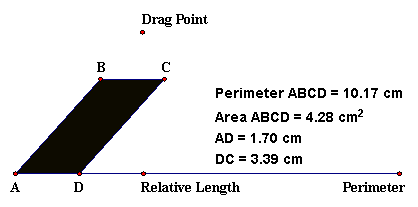
Figure 3.26: Maximum Area for a Parallelogram with Fixed Perimeter

Directed Activity Perimeter vs. Area of Pentagons. Using The Geometers Sketchpad and model 3_MaxPentagonArea.gsp (See Figure 3.27), you may create a variety of pentagons by dragging the vertices. Create several pentagons, each having a perimeter of 12 cm. For each pentagon, note the area. In previous investigations involving triangles and quadrilaterals, what sorts of objects had the maximum area for a fixed perimeter? Describe the pentagon of perimeter 12 cm that you expect to have the largest possible area. Construct that pentagon.

Figure 3.27: Pentagon Perimeters

Directed Activity Inside a Parallelogram. In Figure 3.28, two segments divide the interior of parallelogram ABCD into polygonal regions, diagonal AD and a segment drawn from B to E, the midpoint of side CD. Using the Geometers Sketchpad model 3_ParallelogramProp.gsp, investigate this figure thoroughly. Look for relationships between the areas of the polygons formed in the interior of the parallelogram. Look also for relationships between the segments formed.

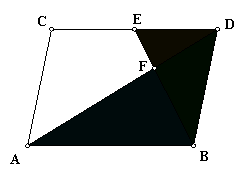
Figure 3.28: Polygons Inside a Parallelogram

Directed Activity Area of a Trapezoid. Like other quadrilaterals, every trapezoid has four sides. Exactly two of the sides, called bases, are parallel. The other two sides, called legs, may or may not be congruent (See Figures 3.29 or 3.30). If the legs are congruent, the trapezoid is called isosceles.

Angles. Like all quadrilaterals, every trapezoid has an angle sum of 360°.

Sides. The perimeter of every trapezoid is computed as the sum of its bases and legs.

Figure 3.29: Trapezoid

Figure 3.30: Isosceles Trapezoid

Area. As suggested by Figure 3.31, the area of every quadrilateral is equivalent to half the area of a parallelogram with a width equal to the sum of the bases of the trapezoid and a height equal to that of the trapezoid. This is sometimes represented as the average of the bases times the height:

Figure 3.31: Area of a Trapezoid

Example 3.2

Find the area of the trapezoid with height = 6cm, base₁ = 8cm, and base₂ = 12cm.

Solution 3.2

Area = .

Directed Activity Perimeter vs. Area of Regular Polygons. Figure 3.32 and Table 3.8 illustrate the relationship between the perimeter and area of a regular polygon. In general, for a polygon with a given radius, the distance from the center of the polygon to a vertex, the both the perimeter and the area increase as the number of sides increases. The sequence of polygons in Figure 3.32 suggests that a regular polygon with 1000 sides would nearly fill the circle in which it is inscribed. Under those circumstances, the perimeter and area of the polygon would approximate the circumference and area of the circle.

Figure 3.32: Perimeter vs. Area of Regular Polygons

Table 3.8 presents apothem, perimeter, and area measurements obtained using The Geometers Sketchpad based on the polygons in Figure 3.32. Note that the area measurements correspond closely with the computed areas obtained using the formula A = 0.5*Apothem*Perimeter, or . If the radii of the polygons are changed, the same relationship is apparent in a numerical analysis. In the case of a polygon with many sides, we may approximate the apothem using the radius of the circle, r, and the perimeter of the polygon using the circumference of the circle, C. Since , we may substitute as follows: . In other words, when a polygon has many sides, its area is close to that of the circle in which it is inscribed.

# Sides	Apothem	Perimeter	Area	0.5ApothemPerimeter
3	1.22	12.65	7.70	7.72
4	1.72	13.77	11.85	11.84
5	1.97	14.31	14.09	14.10
6	2.11	14.61	15.39	15.41
8	2.25	14.90	16.76	16.76
10	2.32	15.04	17.41	17.45

Table 3.8: Computing the Area of a Regular Polygon