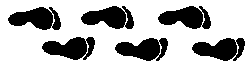Concepts and Connections

Shape

Applications of Symmetry in Art & Design--Concepts & Connections

In Figure 4.27, a dog-like figure is repeated in a one-dimensional decorative pattern called a frieze. Additional friezes are seen in Table 4.8. In architecture, art, and design, friezes are used to decorate the boarders of rooms, floors, ceilings, stationary, and other print materials. Ignoring variations in coloring, what symmetries do you see in these patterns?

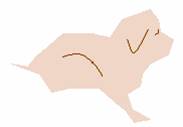
Figure 4.27: Dog Frieze

Table 4.8: Sample Frieze Patterns

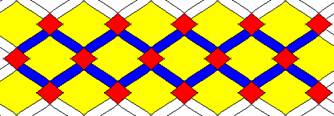
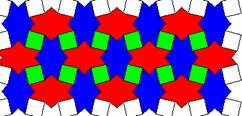
Patterns that repeat in two-dimensions (See Table 4.9) are called wallpapers and are used extensively in the design of wall coverings, carpets, wrapping paper, and printed fabrics. What symmetries do you see in these wallpaper patterns?

Table 4.9: Sample Wallpaper Patterns

A glance at the objects in Tables 4.8 and 4.9 is enough to recognize the existence of repeating patterns. More careful observation suggests the existence of a variety of strategies by which these and other one- and two-dimensional patterns may be generated. At the heart of these strategies are geometric operations called transformations.

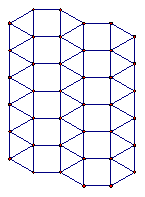
Compositions of transformations may also be used to create interesting designs. For instance, a popular topic in middle school mathematics is tilings. In a tiling, one or more objects are used to cover the plane such that there are no gaps or overlaps. Figure 4.16 shows three different tilings, each based on a different regular polygon: Equilateral triangles, squares, and regular hexagons. Can you think of another polygon, not necessarily regular, that would tile the plane?

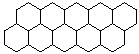
Figure 4.28: Tilings Based on Regular Polygons

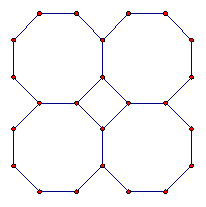
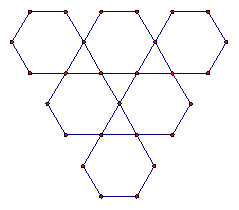
Tilings based on combinations of regular polygons are called semi-regular. Table 4.10 presents four examples. The number sequence associated with each tiling names the n-gons surrounding each vertex. For example, the sequence 4-8-8 indicates that a square and two regular octagons are concurrent at each vertex.

Tiling

Description

4-8-8

3-6-3-6

3-3-4-3-4

3-3-3-4-4

Table 4.10: Semi-regular Tilings

URL

4.5

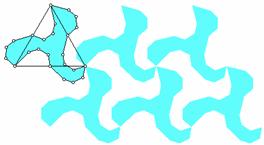
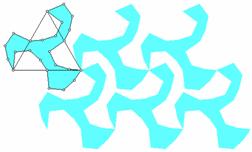
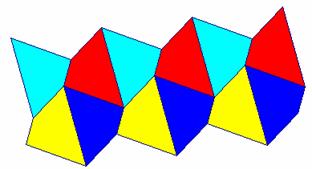
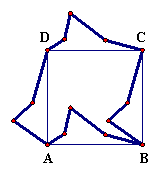
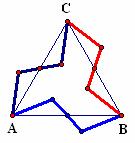
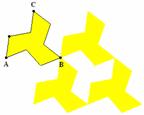
If a single shape is capable of tiling the plane, the tiling is called a tessellation. For instance, the tilings in Figure 4.28 are tessellations, but the tilings in Table 4.10 are not. Surprisingly, there are an infinite number of polygons that tessellate the plane. Figure 4.29 shows a tessellation based on the dog-like object in Figure 4.13. Assuming that you “build” this tessellation starting with the dog in the upper left-hand corner, what transformations would you use to position the other copies as shown?

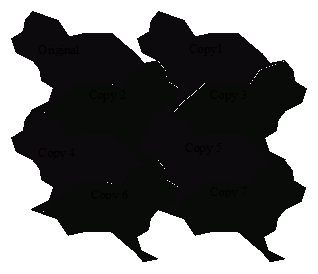
Figure 4.29: Tessellating Dogs

Table 4.11 shows a variety of tessellations, including the dogs seen in Figure 4.29, each created using a different set of transformations. The basic form on which each tessellation is based appears in the upper left hand corner of each figure.

Table 4.11: Sample Tessellations

Making Tessellations

The easiest way to create tessellations is to modify a polygon that, itself, tessellates the plane. For instance, every rectangle, parallelogram, quadrilateral, and triangle tessellates the plane (See Table 4.12).

Table 4.12: Select Tessellating Polygons

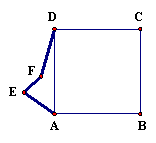
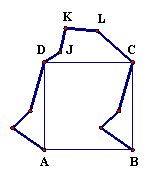
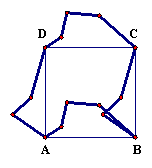
There are many strategies by which a triangle may be modified to create a more complex tessellation. Table 4.13 demonstrates a strategy for creating a tessellation based on the features of square and the operation of translation. The Geometers Sketchpad model 4_Tess.gsp was created using the specified transformations. Beginning with a square, an alternative path between vertices A and D is defined. This path is then translated across the square to the opposite side, BC. A similar procedure is used to define a new path between vertices D and A and to translate the new path from the top to the bottom of the square. At this point (i.e., Step 4), there is a new path between vertices A, B, C, and D. Because this path intersects itself near point B, points on the alternative paths from A to D and from D to C are moved until there are no intersections. The resulting new object (i.e., Step 5) will tessellate the plane. This object is then colored and translated across and down the plane, demonstrating its interlocking features. With a few interpretive marks the new object may be rendered as a dog (See Figure 4.30) or whatever else your imagination suggests.

1. Using the segment tool, draw path AEFD.

2. Select A and B then Mark Vector. Select path AEDF then Translate in the Transform menu.

3. Using the segment tool, draw path DJKLC.

4. Select C and B then Mark Vector. Select path DJKLC then Translate in the Transform menu.

5. If the perimeter of the new object intersects itself, adjust points on the new path to prevent this from occurring.

6. Select the perimeter points of the new object sequentially then select Polygon Interior from the Construct menu. Translate into adjacent positions.

Table 4.13: Square – Translation Strategy

Figure 4.30: Interpretive Markings

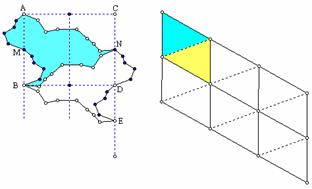
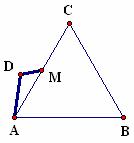
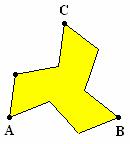
Figure 4.31 shows an equilateral triangle and a new object that will also tessellate the plane. The steps in creating this tessellation are listed in Table 4.14. Note that both the starting shape and the transformations used are different than those employed in Table 4.13.

Figure 4.31: Equilateral Triangle and New Object

	1. Find the midpoint M of side AC.			2. Using the segment tool, draw path ADM.
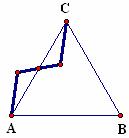
	3. Select point M, then Mark Center and Rotate path ADM 180° in the Transform menu, creating new path AC.			4. Select point C, then Mark Center and Rotate new path AC 60° in the Transform menu to form new path CB.
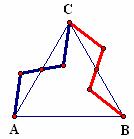
	5. Repeat the same procedures at point B, creating new path BA.			6. Select the perimeter points of the new object sequentially then select Polygon Interior from the Construct menu. Hide all but the indicated points.
	7. Select point A and B then Mark Vector. Select the interior of the new object and then Translate. Repeat using C and B.			8. Adjust the shape of the new object using the unlabeled point.

Table 4.14: Equilateral Triangle - Rotation Strategy

The tessellations demonstrated in Tables 4.13 and 4.14 make use of different strategies to guarantee that the new objects created will interlock perfectly, leaving no gaps or overlaps between adjacent objects. Study each procedure carefully to determine how each strategy achieves this goal. What other strategies could you employ to create tessellations? How could you achieve the same results using paper, pencil, and scissors?

Understanding Friezes

One of the most commonly seen applications of geometric transformation is in friezes. A frieze is pattern of symbols or objects that repeats itself over and over along one dimension. Patterns of this sort are used to decorate the boarders of stationary, at the base or top of a wall, and in advertising. While there are an infinite variety of friezes, all friezes are based on only seven motifs, or frieze groups. Each motif makes use of a different set of symmetries. Table 4.15 illustrates these seven frieze groups using both stick symbols, some of which are recognizable as block letters, and foot prints. After studying these frieze groups, see if you can find any examples of friezes on paper products or integrated into building designs (e.g., patterns in the brinks) and/or decorations.

Sample Group Motifs

Descriptions

LLLLL