Shape 

Copyright David & Cynthia Thomas, 2009

Area--Concepts and Connections

Directed Activity Triangles and Trapezoids.  In this activity, you are asked to determine the area of the triangle seen in Figure 5.17.

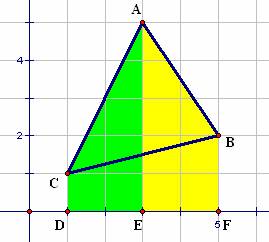
Figure 5.17: Triangle Area

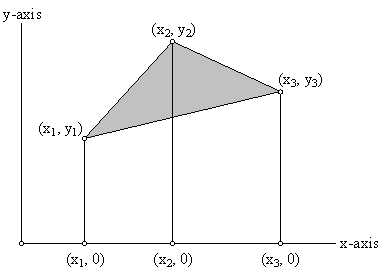
This triangle may be seen as a specific case of a general rule: Any three non-collinear points in the plane determine a triangle (See Geometers Sketchpad model 5_Fig5_18.gsp).  Let the coordinates of the vertices of the arbitrary triangle be represented as.

Figure 5.18: Arbitrary Triangle

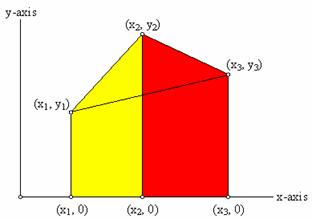
The area of the triangle seen in Figure 5.18 may be written in terms of the areas of three trapezoids seen in Figures 5.19 and 5.20.  The area of the triangle is computed as

Area of Triangle = [Area of Trapezoid 1] + [Area of Trapezoid 2] - [Area of Trapezoid 3].

Figure 5.19: Trapezoids 1 and 2 Trapezoid 1 Vertices:            Trapezoid 2 Vertices:

Figure 5.20: Trapezoid 3 Trapezoid 3 Vertices:

In general, the area of any trapezoid is given by , where b₁ + b₂ represents the sum of the lengths of the parallel bases (i.e., y₁ + y₂) and h represents the height (i.e., the distance between the bases, x₂ - x₁).  Using this approach, the area of ΔABC in Figure 5.18 may be computed using the coordinates of the vertices A(3,5), B(5,2), C(1,1) as follows:

Area of Triangle = [Area of Trapezoid 1] + [Area of Trapezoid 2] - [Area of Trapezoid 3] =

[] + [] - [] = 7 cm².

Directed Activity More Triangles.  In terms of the coordinates of the triangle vertices, the area formula becomes

Area = .

Expanding, simplifying, and arranging terms in this expression yields  as the area of the triangle. 

We now examine a calculation based on matrix algebra and compare results.

Step 1:     Write the coordinates of the triangle's vertices as column vectors in a 3x3 matrix.  Note that the last entry in each column is a 1.

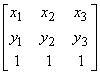
Step 2:     Extend the matrix by repeating the first two columns.  This produces a matrix that has five columns and three rows.  The determinant of this matrix is a number computed as 

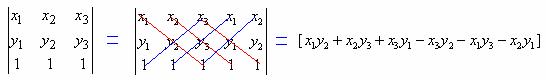
which may be rearranged as .

Step 3:     Compare the expression for area derived using trapezoids to the expression derived using matrix algebra:

Trapezoid Method:

Matrix Method:           =

Step 4:     Note that the result obtained using the trapezoid is equivalent to one-half the negative of the result obtained using the matrix method.  These observations suggests a “shortcut” for computing the area of a triangle: Take half the absolute value of the determinant of the matrix whose column entries are the coordinates of the vertices of the given triangle, entering a 1 in the last row of each column.  Formally, this relationship may be written as:

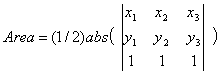
The matrix approach, in addition to its simplicity, produces the area of the triangle directly from the coordinates of its vertices.  As a consequence, there are fewer occasions for introducing errors into the calculation by rounding-off intermediate results. 

Example 5.8

Find the area of the triangle with vertices (3, 1), (5, 6), and (8, 0).

Solution 5.8

The matrix for this problem is written .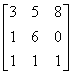 

The determinent of this matrix may be evaluated as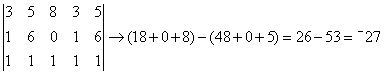

Directed Activity Polygon Area.  Since every n-gon may be divided internally into n-2 triangles, the area of polygon ABCDE may be computed as the sum of the areas of three interior triangles.  Using the matrix method developed in Directed Activity More Triangles, the sum of the areas of three triangles (See Figure 5.21), ΔABC + ΔACD + ΔAED, may be computed from the coordinates of its vertices as 1.5 cm² + 7.5 cm² + 3 cm² = 12 cm².

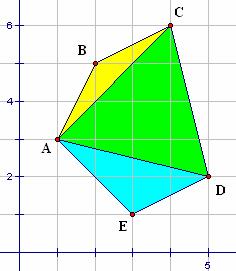
Figure 5.21: Interior Triangles