Shape 

Copyright David & Cynthia Thomas, 2009

Surface Area and Volume--Concepts and Connections

Challenge.  Folding the Circle.

1. Why does this procedure identify the center of the circle?

How do you “fold” a diameter?  Does it matter which diameters you fold?  Why does folding two diameters identify the center of the circle?

Fold a random point on the circle to the center as shown.

Does it matter which point on the circle is folded to the center?  Why or why not?  What is the geometric name for the segment created when you crease the paper?

2. What sort of triangle is created?  The next two folds should create creases that connect to form a triangle.  Achieving this result may involve some trial and error, so don’t fold the paper until it appears that the creases will connect.  Done correctly, this procedure should produce a triangle with three sides of equal length.  What is the geometric name for this triangle?  

3. Why does this procedure work?

Why does the procedure create three sides of equal length?

4. Assume that the large triangle has an area of 1 unit².

This assumption is used to simplify reasoning about areas formed by additional folds.

What is the area of each of the triangles?  Why?

How could you fold the triangle to find the midpoint of each side?  When you have located the midpoints, fold each vertex to the midpoint of the opposite side, creasing the paper as shown.  This divides the original triangle into four triangles.  How are these triangles related?

Fold up the corner triangles to create a regular tetrahedron. 

5. What is the surface area of the tetrahedron?  Why?

How is the surface area of the tetrahedron related to the area of the original triangle?

Unfold the tetrahedron.   Then fold the outside vertex of each corner triangle to the midpoint of its opposite side.

How could you find the midpoints of those sides?

6. What is the area of each small triangle formed in this manner?  Why?

How is area of the small triangles related to the area of the corner triangles?  To the area of the original triangle?

Fold up the large corner triangles and overlap the small corner triangles to create the truncated tetrahedron shown at the left.

7. What is the surface area of the truncated tetrahedron? Why?

Count the area in terms of small triangles then express the surface area as a fraction of the original triangle.

8. What fraction of the tetrahedron’s total volume was lost in the truncation?  Why?

How many small triangles were folded out of sight? 

9. What fraction of the tetrahedron’s total volume remains?  Why?

Imagine that the original tetrahedron is composed of a set of small tetrahedrons, each the size of the tetrahedron truncated (i.e., cut-off) from the original.

Directed Activity The Concept of Volume.

The questions asked in this activity should be discussed with teammates.  Manipulative materials may help you to visualize and describe objects confidently.

Directed Activity The Concept of Surface Area.

The questions asked in this activity should be discussed with teammates.  Manipulative materials may help you to visualize and describe objects confidently.

Directed Activity  The Volume of an Open top Box.

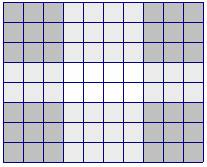
A standard middle school investigation asks students to discover the open top box of greatest volume that may be constructed from a given sheet of one centimeter graph paper.  For instance, each of the 8cm x 10 cm sheets in Table 6.9 may be used to create an open top box by cutting out the darkly shaded corners and folding up the lightly shaded sides. The volume of each box may then be computed as the area of the base times the height of the box or by filing the box with 1 cm³ sugar cubes and counting the volume in unit cubes. The Geometers Sketchpad model 6_BoxVolume, may be used to investigate this phenomenon interactively (See Figure 6.13).  In this model, the size of the sheet may be varied by dragging points B and C, and the size of the corner may be varied by dragging the vertex labeled corner.

As seen in Table 6.9, not all boxes have the same volume.  In this case, two of the boxes have identical volume.  Discovering and interpreting results such as these require an open mind and authentic problem-solving skills.  In this case, the findings suggest that a box of greatest volume may exist with a corner cut of between 1 cm and 2 cm.  This, in fact, is the case. Using calculus, it is possible to determine that the box of maximum volume has a corner cut of approximately 1.48 cm when cut from an 8 cm x 10 cm sheet of paper.  Further experimentation reveals different results for different sized sheets (See Table 6.10) and lays the foundation for an intuitive understanding of the concept of a maximum value. 

Net	Base Area	Height	Volume
	6cm x 8cm  = 48cm^2	1cm	Base x Height = 48cm^2 x 1cm = 48cm^3
	4cm x 6cm  = 24cm^2	2cm	Base x Height = 24cm^2 x 2cm = 48cm^3
	2cm x 4cm  = 8 cm^2	3 cm	Base x Height = 8 cm^2 x 3 cm = 24 cm^3

Table 6.9: Open-top Boxes from an 8cm x 10cm Sheet

	8cm x 10cm  = 80cm^2	1cm	Base x Height = 80cm^2 x 1cm = 80cm^3
	6cm x 8cm  = 48cm^2	2cm	Base x Height = 48cm^2 x 2cm = 96cm^3
	4cm x 6cm  = 24cm^2	4 cm	Base x Height = 24cm^2 x 4cm = 96cm^3
	2cm x 4cm  = 8 cm^2	4cm	Base x Height = 8cm^2 x 4cm = 32cm^3

Table 6.10: Open-top Boxes from a 10cm x 12cm Sheet