Introduction to Fractal Geometry

Problem Statement

This week’s group task involves three tasks centered on the concept of fractals. First, we are to create a fractal using MSW Logo and/or Geometer’s Sketchpad. Secondly, we are to represent the area and perimeter of that fractal both literally and analytically; and finally, we are to write a lesson plan that develops the analysis of these features of the fractal for upper level high school students.

Key Mathematical Concepts

Create a fractal…

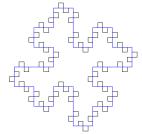
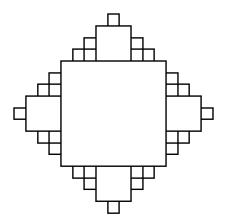
We created the following fractal using MSW Logo. It is a variation on the hat curve, dividing each segment of a square into fourths, then drawing a convex hat on the second fourth of the segment and a concave hat on the third fourth of each segment. Below are sketches of the first 4 levels generated by Logo. The sketches are not drawn using the same scale, but are resized to fit well on this page. The previous curve in each sketch is shown in blue. The code that generates this fractal is attached in a file named mod_hat.lgo and is also shown below the following figure.

1^st level 2^nd level 3^rd level 4^th level

to curve :n

ht

make "x 1

repeat :n [make "x 4*:x]

make "l 200/:x

repeat 4[ifelse :n=0 [fd :l][line :n :l] rt 90]

end

to line :n :l

ifelse :n=1 [fd :l lt 90 fd :l rt 90 fd :l rt 90 fd :l fd :l lt 90 fd :l lt 90 fd :l rt 90 fd :l][line :n-1 :l lt 90 line :n-1 :l rt 90 line :n-1 :l rt 90 line :n-1 :l line :n-1 :l lt 90 line :n-1 :l lt 90 line :n-1 :l rt 90 line :n-1 :l]

end

Analyze the fractal…

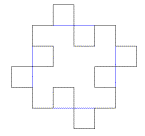
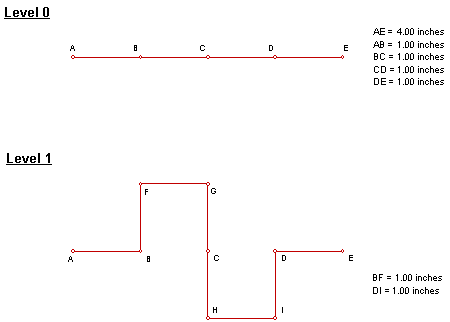
Below you will find an illustration that takes a single side (segment) of the square used to start our fractal and then shows what occurs from that initial level (called level 0) to the following level (this is called the 1^st iteration). The illustration was created by Sketchpad; the file named curve1.gsp is attached. Then following that illustration are descriptions of the analyses we did of the area and perimeter characteristics of this fractal as well as the Excel charts summarizing the information for specific iterations. The Excel file named FractalAnalysis.xls is attached.

…Analysis of Perimeter…

We will start our analysis by looking at perimeter. Perimeter is a function of the length of the sides of a figure, so we will begin by looking at the segments that make up those sides. Geometrically, the sketch above shows that during the 1^st iteration the number of segments making up one of the four sides of our “square” increases from one to eight segments. The Logo code above demonstrates this on line 2 of the “to line” definition. Specifically, the first set of brackets following the ifelse command is responsible for turning one segment into eight. Since one segment becomes eight, the final result is that after each progressive level of iteration our figure is going to have eight times as many segments as it had in the previous level. Analytically, this can be expressed in general terms for the n^th level of the fractal:

Total Segments_n =

You can also note from the sketch that our initial segment AE has a length of four inches. Furthermore, the figure in the level 1 is made up of one-inch segments. If we continued this illustration to level 2, we would be able to note that it was made up of ¼-inch segments. Therefore, segments in the 2^nd level are ¼ the length that they were in the 1^st level and segments in the 1^st level are ¼ the length that they were in level 0. So for any particular level (iteration), each new segment generated is ¼ the length of each segment in the previous level. (This is a recursive definition.) This definition can be expressed explicitly, too, by comparing each iteration back to the initial level. If level 0 is L units long, then level 1 is ¼ of L, level 2 is ¼ of ¼ of L (1/16 of L ), and so on. Since this pattern continues for all consecutive iterations, it allows us to predict a segment length at the n^th level using an equation based on an initial segment of length L:

Length of Segment_n =

In determining the perimeter of our figure as it goes through each additional level, we noted above that a segment in the initial level is L units long. Due to the fact that our figure is a square at this initial level, you simply need to multiply the length of the level 0 segment by four to represent four congruent sides. This leads to the value of 4L. In the level 1 each segment is only ¼ the length of the initial level. However, there are eight times as many segments making up level 1. Therefore, if we multiply the length of a segment found in this level by the number of segments making up our modified “square,” we find that our perimeter for this second level is L/4 * 8segments * 4sides = 8L. If we were to continue on to the next level, we would find that even though the segments making up the figure are only a 1/16 of the original segment’s length, there are sixty-four times as many segments available to contribute to the figure’s perimeter as were found in the initial level. This would contribute to the value of 16L that we calculated (1/16L * 64segments * 4sides). This pattern continues throughout each consecutive level and allows us to derive the perimeter of our figure with an initial segment length of L at the n^th iteration with the equation:

Perimeter_n =

This Excel chart summarizes 10 iterations and their corresponding segments, lengths, and perimeters as discussed above.

N iterations	Total Segments	Segment Length	Perimeter
0	8^0(4) = 4	L/(4^0) = L	(2^2)L = 4L
1	8^1(4) = 32	L/(4^1) = L/4	(2^3)L = 8L
2	8^2(4) = 256	L/(4^2) = L/16	(2^4)L = 16L
3	8^3(4) = 2048	L/(4^3) = L/64	(2^5)L = 32L
4	8^4(4) = 16384	L/(4^4) = L/256	(2^6)L = 64L
5	8^5(4) = 131072	L/(4^5) = L/1024	(2^7)L = 128L
6	8^6(4) = 1048576	L/(4^6) = L/4096	(2^8)L = 256L
7	8^7(4) = 8388608	L/(4^7) = L/16384	(2^9)L = 512L
8	8^8(4) = 67108864	L/(4^8) = L/65536	(2^10)L = 1024L
9	8^9(4) = 536870912	L/(4^9) = L/262144	(2^11)L = 2048L
10	8^10(4) = 4294967296	L/(4^10) = L/1048576	(2^12)L = 4096L
N	(8^n)*4	L/(4^n)	(2^(n+2))*L

Finally, as we look at the perimeter of the fractal after an infinite number of iterations, we can conclude that the perimeter increases without bound.

…Analysis of Area…

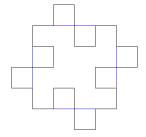
Now we will analyze the area of the fractal. Geometrically, the sketch above allows us to determine how many squares are added and subtracted for this, the first iteration. It can be seen that for every segment of the original blue square, there is a new square added to the outside and another square taken away from the inside. Since the original figure (level 0) has 4 segments, there is a total of 4 squares added to the outside and 4 squares of equal size missing from the inside of the next figure (level 1). Due to the “convex” and “concave” nature of each subsequent iteration, we are in a sense adding a square and then taking away a square for each segment of the previous figure. Therefore, all iterations add and subtract an equivalent number of squares. This helps make this constructive property task fairly trivial. The number of squares being added and subtracted at the n^th iteration is dependent on the number of segments at the (n-1)^th iteration. Therefore, we can utilize our results for the number of segments above and write the equation:

Due to the fact that for every square that is added to our figure, there is another square of equivalent area that is being subtracted from it as well, it stands to reason that we will not be adding any area to our figure throughout our transformations. Analytically, if the area of the original square is assumed to be one square unit, the additional area contributed by the nth-iteration is also given by the following expression and results in an unchanged area.

The sum of the areas of all such contributions plus the area of the original square is given by the expression:

N	Segments	Squares Added	Additional Area
0	4
1	32	32*1-32*1	0
2	256	256*1-256*1	0
3	2048	2048*1-2048*1	0
4	16384	16384*1-16384*1	0
5	131072	131072*1-131072*1	0
6	1048576	1048576*1-1048576*1	0
7	8388608	8388608*1-8388608*1	0
8	67108864	67108864*1-67108864*1	0
9	536870912	536870912*1-536870912*1	0
10	4294967296	4294967296*1-4294967296*1	0
n	4*8^n	4*[8^(n-1)]-4*[8^(n-1)]	0

Taking the limit of this expression as n goes to infinity yields

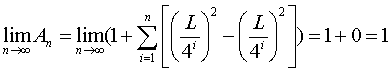
We can see through this analytical approach that it supports what we concluded geometrically; there is no change in area.

In conclusion, while the perimeter of our fractal becomes infinitely large after an infinite number of iterations, its area is not affected by any number of iterations.

Write a lesson plan…

Overall description:

The students will investigate fractals in small groups and individually. It is assumed the students are on the 11^th or 12^th grade level and have been introduced to the concept of self-similarity at a previous time. The students have the needed technology skills to use the software/calculators described in this lesson. This lesson could serve as an application/review of sequences and series or as a stand-alone section on analyzing patterns.

Time Frame:

2-3 50-minute periods or 1-1½ blocks (includes assessment, but not the extended assignment).

Objectives:

1) Each student will be able to verbally and accurately describe the generator of a fractal.

2) Each student will use inductive reasoning to discover patterns in area and perimeter of the fractals and use those patterns to find the area or perimeter of any level of a fractal.

3) Each student will derive algebraic formulae to express the area and perimeter of the n^th level of iteration of a fractal.

4) Each student will have opportunity to apply what they have learned through an extension topic using the graphing calculator.

Introductory discussion (Anticipatory Set):

The teacher will review the concept of self-similarity. The anticipatory set handout is attached in a file named AntSet_SelfSim.doc and is included in print form at the end of this lab report. The term recursion will be introduced or reviewed as needed. Analogous examples to help students understand might include looking in a mirror while holding a mirror or taking a picture of someone taking a picture of you taking a picture of them… The teacher should point out or have students point out weaknesses to the analogy, such as reflections grow smaller overall while fractals do not necessarily do so.

Modeling of concept:

The teacher will model generating 2-3 iterations of a fractal using Koch’s snowflake. This can be done with MSW Logo (the Logo file is attached as koch.lgo) or the Geometer’s Sketchpad or by hand using an overhead projector or chalkboard. He/she will guide the students to understand what is being asked when the activity sheet says to “verbally describe the generator” and “investigate area and perimeter”. No development of formulae will take place in the modeling stage, as discovery is the purpose of the exploration.

Exploratory activity:

The students will work in pairs or small groups using MSW Logo or Geometer’s Sketchpad to generate different fractals. The fractal introduced above (modified hat fractal, attached as mod_hat.lgo) will serve as the initial investigation. Files will be provided that include the programs or scripts needed for students to choose at least one additional fractal to investigate. (Right now there are 3 files listed from which to choose; ideally there would be 4 or 5.) The emphasis of this exploration is determining area and perimeter relationships in fractals both recursively and explicitly. The software will also assist students in giving verbal descriptions of the fractal generator. An activity sheet will assist the students in organizing the information they discover during the exploration. This sheet is attached in a file named Fractal_Explore.doc and is included in print form at the end of this lab report.

Assignment:

The students will receive a take-home assignment including 2 fractals to analyze individually (similar in nature to those done in the group session) as well as specific iterations to evaluate for given formulae. Students will also be asked to describe in writing the fractal generator of the 1-2 fractals analyzed as well as be prepared to give an oral description in class. As a challenge assignment, students can be encouraged to generate their own fractals using software if available or graph paper if not. The take-home assignment sheet is attached in a file named Fractal_TakeHome.doc and is included in print form at the end of the lab report.

Assessment:

In-class group work (objectives 1-3): This portion of the lesson will be worth 25 points. The teacher will listen for and log examples of constructive participation during the activity. Points will be assigned for participation as follows:

Minimal--present, but no meaningful contributions = 10 pts

Average--follows directions doing the very least possible = 15 points

Above average--meets all requirements = 20 points

Superior--exceeds requirements, initiates additional investigations = 25 points

Take-Home assignment (objectives 1-3): This portion of the lesson will be worth 50 points. Students will contract for the grade they wish to attain as follows:

C—correctly complete guidelines listed on handout for 2 fractal patterns

B—complete C grade requirements plus create and analyze 1 original fractal

A—(includes objective 4) complete B grade requirements plus complete the Extension handout (the extension assignment is due at the beginning of the 4^th class period following the completion of the exploration).

In a class session following the completion of the exploration and take-home assignment, students will be asked to give an oral description of a fractal to the class (or group within the class). The group will attempt to draw the fractal from the description given. Group drawings will be used to assess the student’s success; this portion will be worth 10 points. A short class discussion as well as written work will be used to assess those students who chose to complete the extension assignment, thus giving the students opportunity to verbalize what they learned and allowing the other students to benefit from the assignment as well. Points (which make the difference between a B grade and an A grade) will be applied to the individual student’s contracted grade.

Extension:

By choosing this extension, each student will have opportunity to learn about fractals and chaos theory in the context of a game. The teacher will introduce the activity with examples of natural phenomena that can be modeled using self-similarity and will provide a handout with the needed information. This assignment will be completed outside of class and will be due at the beginning of the 4th class period following the completion of the exploration. A copy of the handout can be found at the end of this lab report; the file is attached as chaos.doc.

Enrichment:

Interested students may further investigate fractals by using the website http://www.math.rice.edu/~joel/paperfractal/. Individual students may contract with the teacher for additional points by preparing an oral or written report after a thorough study of this website.

Technology Used

We used MSW Logo to create fractals for both our investigation/analysis and the planned high school activities. Microsoft Excel was used to assist in analysis of the perimeter and area formulae. In preparing this report, we used the Geometer’s Sketchpad to create a sketch showing the fractal generator for our modified hat fractal and a freeware program named PrintKeyPro to do a screen capture of the Logo drawings used for our illustrations. In addition, the student extension activity calls for the use of a graphics calculator; specifically the code is written for a TI 83.

Principle Finding

We were able to create, analyze, and write lessons focusing on specific properties and concepts of fractals and self-similarity. The analysis was made much easier by the geometrical representation of the fractal using Logo. Because of the area/perimeter features of Sketchpad, we believe it would make a valuable tool for analyzing fractals as well. We simply did not have time to investigate both avenues, Logo and Sketchpad, separately. We found it challenging to write a lesson plan as a group. With four people contributing, it is difficult to design a lesson for just one class period; there are far too many good ideas floating around!

Summary and Applications

The study of fractals is fascinating as it shows a “new” development in mathematics. Most students think of math as old and static; this lesson would give them an opportunity to see the progress being made in the recent past and how it can be applied in areas that interest them (such as computer animation in movies and video games). The analysis of the Logo code for students familiar with programming would provide an excellent study in recursion. Original programming would offer a student the opportunity to operate on the synthesis/analysis level of learning. When you write code, you have to know what’s going on. However, students could benefit from the use of pre-written programs as well. Any visual representation would assist in making a verbal description of the fractal as well as making conjectures about area and perimeter.

The following pages are copies of the handouts used for the high school lesson plan.

Self-Similarity? Oh, yes…Self-Similarity!

Topic: Fractal Trees

Materials: Isometric dot paper

Use your own isometric dot paper and make a fractal tree. Look for patterns. Be prepared to discuss what you notice. What would you have to do to make a larger fractal tree?

Do you remember?

When small parts of the fractal tree are magnified, detail is not lost. In fact the magnified part looks the same as the entire structure. This is called self-similarity. One of the characteristics of a fractal is that it exhibits self-similarity. The picture below demonstrates this.

Put this handout in your notebook for easy reference.

Name _____________________

Fractal Exploration

In this exploration, you will be investigating the area and perimeter of fractals. You will also be practicing your communication skills by verbally describing how the fractal is generated. You will complete this exploration with a partner; both of you must contribute to the activity in order to earn full credit. Your teacher will be available to assist, but this is an exploration…a search for unknowns…so don’t expect the teacher to have all the answers!

This exploration is worth 25 points. Your teacher will be listening and watching for log examples of constructive participation during the activity. Points will be assigned for participation as follows:

10 pts – Minimal – you are here, but make no meaningful contributions

15 pts – Average – you follow directions, but does the very least possible

20 pts -- Above average -- you meet all requirements and demonstrate independent initiative

25 pts – Superior – you exceed the requirements, initiate additional investigations

So, let’s get started!

Phase 1: Explore a modified “hat” fractal.

After starting MSW Logo, open the file mod_hat.lgo. Each of the fractals in this exploration are run (after loading), by typing curve n, where n is the iteration level you want to see.

Explore. Use the space below to write a description of how the fractal is generated. (That means someone listening to your description could draw the fractal without ever seeing a picture of it.)

Use the table to help keep track of the facts listed. Remember, you are looking for patterns.

Curve n	Number of Segments	Length of each segment	Perimeter of figure
0
1
2
3
4
5
n

Need a hint? As you look for patterns, try asking these questions…

• How does 1 segment compare in length to a segment in the figure before?
• How does the number of segments change each time?
• How does length of segments and number of segments affect perimeter?

Can you write both recursive and explicit formulae for this fractal? Do you remember the difference? Use the space below to impress me!

Now do the same thing you did above, only look for patterns in the area of the shape.

Curve n	Number of segments	Shapes added or taken away	Additional area	Area of figure
0		0
1
2
3
4
5
n

Phase 2: Explore another fractal

Now you can explore another fractal. Choose from the following list:

haton_rt.lgo

halfhat_rt.lgo

pentfrac.lgo

After you pick one that interests you, complete the following tables in the same manner you did Phase 1.

Use the space below to write a description of how the fractal is generated.

Curve n	Number of Segments	Length of each segment	Perimeter of figure
0
1
2
3
4
5
n

Curve n	Number of segments	Shapes added or taken away	Additional area	Area of figure
0		0
1
2
3
4
5
n

Fractal Take-Home Assignment

This assignment is worth 50 points. It is due at the beginning of our next class period. You may contract for the number of points you want to earn as listed below:

C—correctly complete the 2 fractals on this handout according to the guidelines given

B—C grade requirements plus design and analyze a fractal of your own making. You may use Logo, Sketchpad, or draw at least 3 iterations by hand.

A—B grade requirements plus complete the Extension handout (the extension assignment is due at the beginning of the 4^th class period following the completion of the exploration).

Part I

Consider this hat fractal. Analyze it as you did the fractals in the exploration activity. Write the following formulae in terms of n, where n is the number of iterations completed:

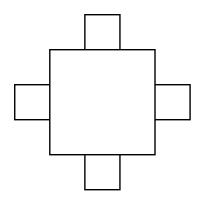
Number of segments:

Length of each segment:

Perimeter of shape:

Squares added:

Area of total figure:

Use your formulae to answer these specific questions.

1. What is the area of the fractal after the 3^rd iteration?

2. What is the perimeter of the fractal after the 4^th iteration?

3. What do you think happens to the perimeter of the fractal as n increases without bound?

4. Does the area behave in the same way? Give evidence to support your answer.

Write a description of how the fractal is created.

Part II

Consider this triangular fractal. Analyze it as you did the fractals in the exploration activity. Write the following formulae in terms of n, where n is the number of iterations completed:

Number of segments:

Length of each segment:

Perimeter of shape:

Triangles added:

Area of total figure:

Use your formulae to answer these specific questions.

5. What is the area of the fractal after the 8^th iteration?

6. What is the perimeter of the fractal after the 10^th iteration?

7. What do you think happens to the perimeter of the fractal as n increases without bound?

8. Does the area behave in the same way? Give evidence to support your answer.

Write a description of how the fractal is created.

Extension

Fractal geometry is a branch of chaos theory, which can be used to describe natural phenomena. Traditionally, it has been thought that some patterns are impossible to describe through mathematical modeling. One area in which we found these “impossible” patterns is geography. However, this new (when you consider the history of math) branch of mathematics has proven tradition wrong! A photograph from space of mountain foothills might have fractal self-similarity. The coastline of a island can be modeled with fractals. This extended assignment focuses on a chaos game. Almost everyone loves to play games, so let’s see how chaos theory works in relation to fractals.

THE GAME: Chaos

First draw an equilateral triangle on a piece of paper. Label the vertices of the triangle T, R, and L to represent top, right, and left. Choose any point x in the interior of the triangle as the starting point. Roll a die to choose T, R, or L at random. Then plot the point that is half way to the vertex that has been selected. Continue to roll a die to choose vertices and plot points.

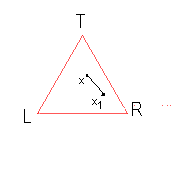
Do you see a pattern? Probably not at first! Could a random selection of points produce anything? Why not let modern technology serve as a tool in helping you answer that question. You can program a graphing calculator to play the game of chaos with the following directions.

The following program generates 3000 points in a chaos game. (Much easier than playing chaos by hand!)

PROGRAM: SIERPINS

:FnOff :If 1/3<N and N£2/3

:Clrdraw :Then

PlotsOff :.5(.5+X)àX

:AxesOff :.5(1+Y)àY

:0àXmin: 1àXmax :End

:0àymin: 1àymax :If 2/3<N

:randàX: randàY :Then

For (K, 1, 3000) :.5(1+X)àX

randàN :.5YàY

:If N£1/3 :End

:Then :Pt-On (X, Y)

:.5XàX :End

:.5YàY :StorePic 6

:End

Describe the pattern produced by this game.

Do you think this pattern might be a fractal? Explain.

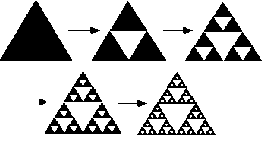
Compare the picture generated by the above program with the sketches below. These sketches illustrate a fractal called the Sierpinski’s triangle. It was named after the Polish mathematician Waclaw Sierpinski who introduced it in 1916.

Describe a recursive process to draw the Sierpinski Triangle.