Solutions to Selected Odd-numbered Exercises
Section
1.1
1.
In
the Egyptian approach, ![]() . In the Babylonian
approach,
. In the Babylonian
approach, ![]() , which is closer to the actual value. So, the Babylonians had a more accurate method
for computing the area of a circle.
, which is closer to the actual value. So, the Babylonians had a more accurate method
for computing the area of a circle.
3.
![]()
![]()
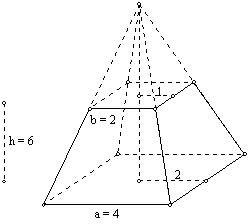
Using similar triangles, compute the volume of the
small pyramid and the large pyramid as
Large pyramid = ![]() Small
pyramid =
Small
pyramid = ![]()
Large pyramid volume - small pyramid volume = 64 - 8
= 56. The procedure computes the volume
of the truncated pyramid.
5.
a) Answers may vary, such as 6, 8, 10; 5, 12,
13; 10, 24, 26
b) ![]() , which leads to the triple 3, 4, 5.
, which leads to the triple 3, 4, 5.
c) ![]() Since n is always an
integer, k must always be irrational.
Consequently, no integer values of k are possible.
Since n is always an
integer, k must always be irrational.
Consequently, no integer values of k are possible.
d)
Pythagorean triples take the form ![]() , where m and n are integers such that gcd(m,n) = 1. If
, where m and n are integers such that gcd(m,n) = 1. If ![]() then we are done. If
3 does not divide m and 3 does not divide n, then m = 1(mod3) or m = 2(mod3) and n = 1(mod3) or n = 2(mod3). If m = 1(mod3), then m2 =
1(mod3). Likewise, if m = 2(mod3), then
m2 = 1(mod3). [Why?] Similar argument applies to n. Then m2 - n2 = 1 - 1 =
0(mod3). So, m2 - n2 is divisible by 3.
then we are done. If
3 does not divide m and 3 does not divide n, then m = 1(mod3) or m = 2(mod3) and n = 1(mod3) or n = 2(mod3). If m = 1(mod3), then m2 =
1(mod3). Likewise, if m = 2(mod3), then
m2 = 1(mod3). [Why?] Similar argument applies to n. Then m2 - n2 = 1 - 1 =
0(mod3). So, m2 - n2 is divisible by 3.
7.
Assume
that ![]() is rational. Then
is rational. Then ![]() , where p and q are integers. Furthermore, we may assume that p and q have no common
factors. Squaring both sides yields
, where p and q are integers. Furthermore, we may assume that p and q have no common
factors. Squaring both sides yields ![]() This forces p2
to be even, which forces p to be even.
If p is even then p2 is divisible by 4. This forces 2q2
to be divisible by 4. Therefore, q2
must be even, forcing q to be even.
Since p and q are both even, then have a common factor, contradicting
the assumption. So
This forces p2
to be even, which forces p to be even.
If p is even then p2 is divisible by 4. This forces 2q2
to be divisible by 4. Therefore, q2
must be even, forcing q to be even.
Since p and q are both even, then have a common factor, contradicting
the assumption. So ![]() cannot be rational.
It is irrational.
cannot be rational.
It is irrational.
9.
![]() is the total area
within the figure. The four rectangles
have a total area of 4ab. The square in
the interior of the figure must then have an area of
is the total area
within the figure. The four rectangles
have a total area of 4ab. The square in
the interior of the figure must then have an area of ![]() -4ab = (a-b)2.
Consequently, (a+b)2 > (a-b)2.
-4ab = (a-b)2.
Consequently, (a+b)2 > (a-b)2.

11.
1+2+3+
... = n(n+1)/2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Section
1.2
1.
Answers
will vary.
3.
Answers
will vary.
5.
a) Model
Points A,
B, C
Lines A
B A
B C
C
A1: Note
that there are exactly 3 points.
A2: Note
that every pair of points is represented as a column (e.g., as a line).
A3: Note
that
- lines AB and BC have B in
common.
- lines BC and AC have C in
common.
- lines AB and AC have A in
common.
A4:
Note that no line contains more than 2 points.
So, the system is consistent
b)
The following models may be used to demonstrate
the independence of the axioms:
|
Model 1 A D D
D B A B
C C |
Model 2 A A B C |
Model 3 A B C |
Model 4 A B A
C B C C |
Section 1.3
1.
Answers will vary.
3.
a)
![]()
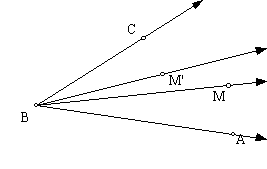
Assume there are two distinct midpoints,
M and M'. Since M and M' are midpoints
of segment AB, d(AM) = d(MB)= .5d(AB).
Furthermore, d(AM) + d(MB) = d(AB) and d(AM) + d(MM') + d(M'B) =
d(AB). Since d(M'B) = .5 d(AB) = d(AM),
d(AM) + d(MM') + d(M'B) = d(AB) + d(MM') = d(AB), so d(MM') = 0. Consequently, M and M' are not distinct and
there is only one midpoint.
b)
Use the same approach taken in part a), this time in terms of angle
sums.
c)
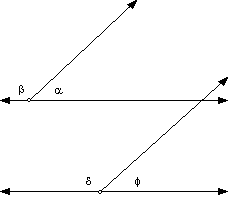
Let a = f. Since 180° = a + b = f +
d, b = d. A similar argument applies
to angles complementary to congruent angles.
d)
Let line m intersect side BC at point P. Then B and C are on opposite sides of line m. Assume that m does not intersect sides AB or
AC. Then A and B must be on the same
side of line m. Likewise, A and C must
be on the same side of line m. Then, by
transitivity, B and C must be on the same side of line m. Consequently, line m must not intersect side
BC, which is a contradiction.
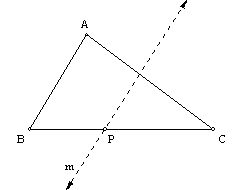
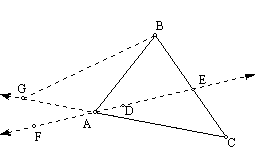
e)
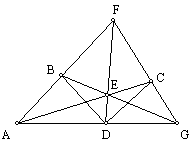
Extend AD from A to form line FD.
Extend AC to a point G and draw segment GB. Consider DGBC. By Pasch, ray AD must intersect either BG or
BC. Because point D is in the interior
of ÐBAC, all points
of the ray AD are in the interior of the angle. Since no points of BG are in the interior of the angle, ray AD
must intersect BC.
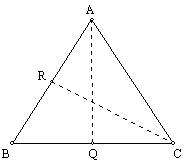
f)
Let Q be the midpoint of BC and R the midpoint of BA. Draw segment AQ. DABQ @ DACQ by
side-side-side. Then ÐABC @ ÐACB. Draw segment CR. DCRB @ DCRA by
side-side-side. Then ÐABC @ ÐBAC.
Section 1.4
1.
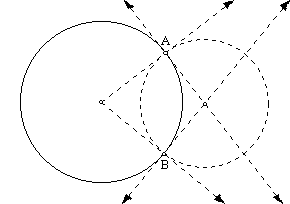
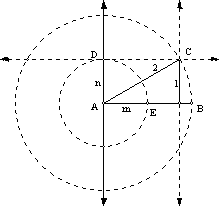
a) Let m ^ n at point A. Construct a circle with center A and radius
AB. Find the midpoint of AB, point
E. Construct a circle with center A and
radius AE. Let point D be the
intersection of that circle and line n.
Construct a line parallel to AB through D. Label the intersection of that line and the larger circle point
C. Ray AC forms a 30° angle with line
m, since the sine of ÐBAC = 0.5. To
complete the trisection, bisect ÐCAD.
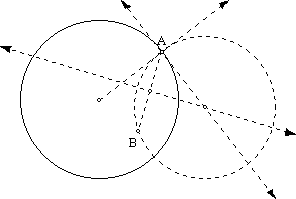
b)
Construct a perpendicular to line AB at C. Bisect ÐDCB. This completes the trisection.
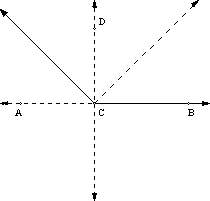
c)
Given ÐCAB = 45°, construct an
equilateral triangle DDEF and bisect ÐDEF, forming ÐFEG = 30°. Copy ÐFEG at point A so that EF overlaps AB. Bisect ÐGAB to complete
the trisection.
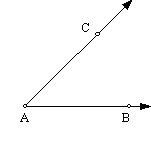
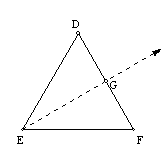
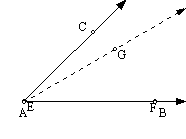
3.
Starting with the demonstration of this problem seen on the first
screen of the Modern Geometry CD-ROM, complete the task by finding the
geometric mean of the two sides of the triangle (See Figure 1.4.14) created in
that demonstration.

5.
DABC ~ DAED, so 1/b -
a/x. Then x = ab.
7.
DCBD ~ DDBA, so 1/x =
x/a. Then x2 = a, so x = ![]() .
.
9.
x3 - 2 = 0. By
the rational root theorem, there are no rational roots to this equation, nor
would any composition of square roots yield the necessary result.
Section 2.1
1.
Answers will vary
a.
STEP ACTION
1 Using
a compass, mark points D and E on the sides of angle BAC such that DA=EA.
2 Draw
a segment from D to E.
3 Using
the length of segment DE as a radius, construct arcs centered at D and E and
mark
their
point of intersection as point F.
4 Draw
segments FD and FE.
5 Dray
ray AF
b. STEP ACTION
1 Using
the length of segment AB as a radius, construct arcs centered at A and B and
mark
their
point of intersection as point C.
2 Using
the procedure described in Proposition 9, bisect angle ACB.
3 The
bisector of angle ACB also bisects segment AB.
c. STEP ACTION
1 Using
point C as the center, construct arcs of equal radius on either side of C. Mark the
points of
intersection of these arcs with line AB as points D and E.
2 Using
the procedure described in proposition 1, construct an equilateral triangle
with side
DE
as the base. Label the third vertex of
this triangle as point F.
3 Draw
segment FC. This segment is
perpendicular to AB at point C.
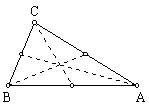
3.
STEP ACTION
1 Using
the procedure described in Proposition 10, find the midpoint of segment AB.
Label the midpoint
F.
2 Repeat
the same procedure on segments BC and AC.
3 Draw
segments AD, BE, CF
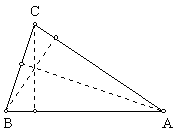
5.
STEP ACTION
1 Using
the procedure described in Proposition 12, draw a perpendicular line from point
C
to the line
containing segment AB
2 Repeat this procedure to draw
perpendicular lines from the other two vertices to the lines
containing
the other two sides of the triangle.
Section 2.2
1.
a) No
b)
Yes, the midpoint of the hypotenuse of a right triangle.
c)
The "center" of the triangle coincident with the incenter and
centroid.
3.
Answers may vary, for instance:
![]()
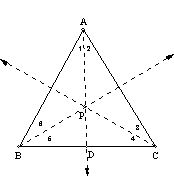
5.
Equilateral triangles.
Since the incenter is always in the interior of a triangle and the
circumcenter
Is in the interior only for acute
triangles, only acute triangles need be considered. Let P be the incenter of triangle ABC. Then Ð1 = Ð2; Ð3 = Ð4; Ð5 = Ð6. If P is also the circumcenter, then AP ^ BC and DADB @ DACD by
angle-side-angle. Consequently, AB =
AC. Using similar reasoning, AC =
BC. Then AC = AB = BC and the triangle
is equilateral.
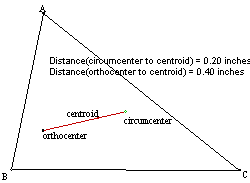
7.
The centroid is always between the orthocenter and
circumcenter. The distance from the
orthocenter to the centroid is twice the distance from the circumcenter to the
centroid.
Section 2.3
1.
Answers will vary.
3.
Answers will vary.
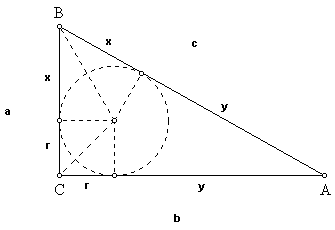
5.
a = r + x ® x = a - r; b = r + y ® y = b - r; c = x + y
a2 + b2 = c2; (r + x)2 + (r + y)2 =
(x + y)2 ® (r2
+ 2rx + x2) + (r2 + 2ry + y2) = x2
+ 2xy + y2 ®
2 r2 + 2rx + 2ry = 2xy ® r2 +
rx + ry = xy ® r2 +
r(x + y) = xy. Then r2 + rc
= (a-r)(b-r) ®
r2 + rc = ab -ar -br + r2,
so rc = ab - ar - br ® rc + ra + rb =
ab ® ![]()
7.
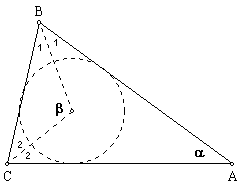
a = 180° - 2(Ð1 + Ð2) ® Ð1 + Ð2 = (180° - a)/2
b = 180° - (Ð1 + Ð2) ® 180° - (180° - a)/2 = 90 - a/2
Section 3.1
1.
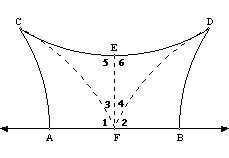
DCAF @ DDBF by
side-angle-side. So CF @ DF and Ð1 @ Ð2. Then DCFE @ DDFE by
side-side-side. Then Ð1 @ Ð4 Ð5 @ Ð6. Since Ð5 + Ð6 = 180°, Ð5 = Ð6 = 90°. Then Ð1 + Ð3 = Ð2 + Ð4 ® ÐAFE and ÐBFE are right
angles so EF ^ AB.
3.
Logical equivalence is established by proving each statement from
the other.
a)
|
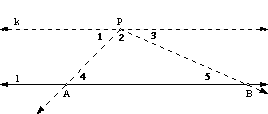
Playfair: Through a
point not on a given line exactly one parallel may be drawn to the given
line.
Given: Line k is parallel to line l through point P. Proof: Construct rays PA
and PB through point A and B on l.
Label the angles formed as shown.
Ð1 + Ð2 + Ð3 = 180°. Since k is parallel to l, we know that Ð1 = Ð4 and Ð3 = Ð5. Then Ð4 + Ð5 + Ð2 = 180°. |
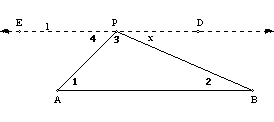
The sum of the angles of any triangle is equal to 2 right
angles.
Given: Ð1 + Ð2 + Ð3 = 180°. Proof: Copy Ð4 at point P
as shown. Label a point E on the side of Ð4 as shown, to the left of P.
Since Ð4 = Ð1, line l is
parallel to AB. Draw a line through
EP, forming Ðx. Then Ð4 + Ð3 + Ðx = 180°. (We must now show that this is the same
parallel obtained if Ð2 is copied at
point P to form Ðx.) Since Ð1 = Ð4 and Ð4 + Ð2 + Ð3 = 180°, Ð2 = Ðx. Thus, the line through P drawn parallel to
AB because Ð1 = Ð4 is the same
line drawn through P parallel to AB because Ð2 = Ðx. So there is only one line parallel to AB
through P. |
b) - d) are
demonstrated using the same general approach.
Section 3.2
1.
|
|
|
|
|
|
|
|
|
3.
Answers will vary.
5.
C = 2psinh(R) = 2psinh(2) =
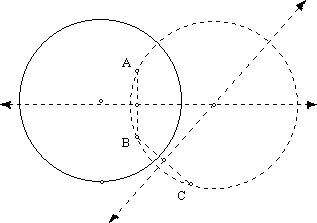
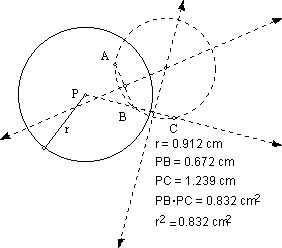
22.79; C = 2psinh(R) = 2psinh(4) = 171.47
7.
If the center of the
circle is O and the distance from O to A is r, 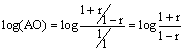
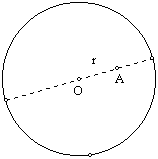
Section 3.3
1.
Defect = 180° - 153° = 27°
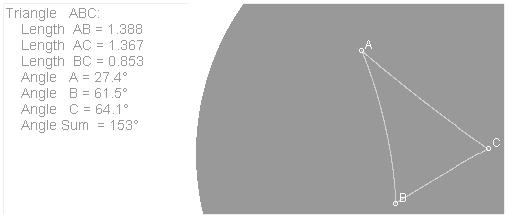
3.
cosh(c) =
cosh(a)*cosh(b) = cosh(2)*cosh(3) =
37.88 ® c = 4.327
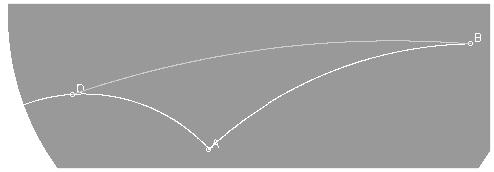
5.
Answers will vary.
7.
The legs of a Saccheri quadrilateral are perpendicular to the
base. The base is a common
perpendicular between the sides. Assume
that a second common perpendicular existed.
It would complete a rectangle with the base and sides, a figure that is
not possible in this space. So the
segment joining the midpoints of the sides cannot be perpendicular to the
sides.
9.
cosh(1)*cosh(BC) = cosh(3) ® BC = 2.56
11.
Answers will vary, but resemble the proof of Case 1.
13.
Begin with any two non-intersecting lines l and m. since there is only one common perpendicular
between l and m, forming two right angles, no second common perpendicular is possible to complete the rectangle.
15.
Since the shortest distance between two non-intersecting lines is
along a common perpendicular, and since there is only one common perpendicular
between such lines, all other separations are different. Consequently, no all separations are the
same.
17.
Since the sum of the interior angles is less than 360° and the sum of
the three given angles is 270°, the fourth
angle must be acute.
19.
Area DABD + Area DADC = Area DABC. Since area = defect, Defect DABD + Defect DADC = Defect DABC.
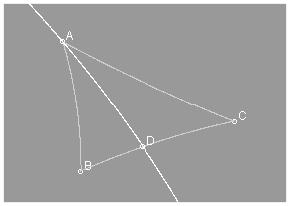
21.
Area DABC > Area DDEF so Defect DABC > Defect DDEF
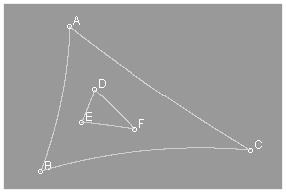
Section 3.4
1.
By Theorem 3.4.1, if ÐH = ÐI, ÐC = ÐD, and if ÐA = ÐB, the triangles
are congruent. Since all lines are
orthogonal to the bounding circle, the angles formed at omega points A and B
both have measure zero. Consequently,
the triangles are congruent.
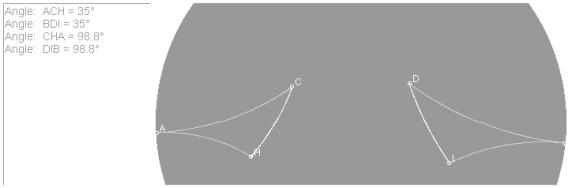
3.
DADB @ DADC by Theorem
3.4.3. Then ÐBDA @ ÐCDA, so AD ^ BC.
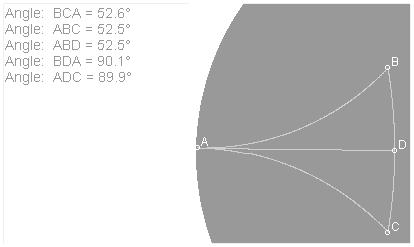
5.
Ð1 + Ð2 + Ð3 = Ð4 + Ð5 + Ð6 is true only
in Euclidean space.
Section 4.1
1.
a.
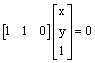
b.
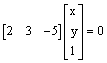
c.
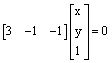
d.
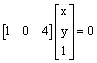
e.
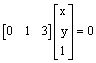
3.
a.
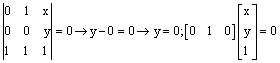
b.
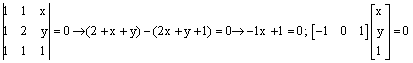
c.
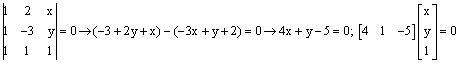
d.
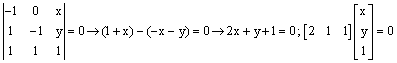
5.
Answers will vary.
7.
To prove this theorem, simply restate Example 4.1.1 with suitable
discussion.
9.
Let ![]() . Eliminating x using
linear combination, one obtains
. Eliminating x using
linear combination, one obtains ![]() . Eliminating y using
the same approach yields
. Eliminating y using
the same approach yields ![]() . Now expand
. Now expand 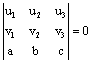 to obtain
to obtain ![]() . Regrouping terms
yields
. Regrouping terms
yields ![]() . Dividing each term
by
. Dividing each term
by ![]() and expressing the
result in matrix form yields
and expressing the
result in matrix form yields
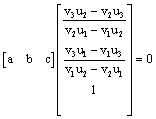 . So, the matrix
procedure yields the correct results as determined by the method of linear
combination.
. So, the matrix
procedure yields the correct results as determined by the method of linear
combination.
11.
Consider two lines ![]() . From analytic
geometry, any line perpendicular to the line y = mx+b has slope –1/m.
Since the slope of line u is given by
. From analytic
geometry, any line perpendicular to the line y = mx+b has slope –1/m.
Since the slope of line u is given by ![]() , the slope of any line perpendicular to u must have slope
, the slope of any line perpendicular to u must have slope ![]() . Therefore, the
slope of line v, given by
. Therefore, the
slope of line v, given by ![]() , must equal
, must equal ![]() . If
. If ![]() =
=![]() , then
, then ![]() .
.
Section 4.2
1.
a.
![]()
b.
![]()
c.
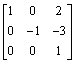
d.
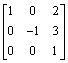
e.
![]()
f.
![]()
g.
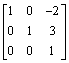
h.
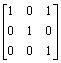
i.
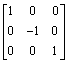
j.

k.
![]()
l.
![]()
3.
ku’ = uT-1
5.
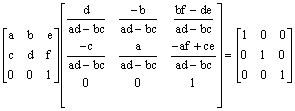
7.
Answers will vary.
Section 4.3
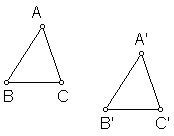
1.
3.
![]()
5.
Geometric thinking: Under rotations, only the turn center is
invariant. So the only invariant point
for this transformation is the origin.
Since rotations do not have invariant lines, there are none for this
transformation.
Matrix methods: 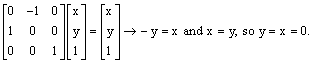 Consequently, the
origin is invariant under this transformation.
Since
Consequently, the
origin is invariant under this transformation.
Since 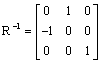 ,
, 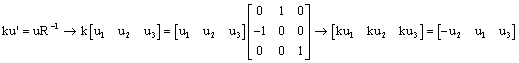
Letting k=1, this leads to [0 0 u3],
which isn’t a line, so there are no invariant lines.
7.
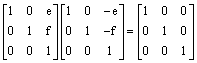
9.
Given two points ![]() and
and ![]() , the distance between them is given by
, the distance between them is given by ![]() .
.
A rotation about the origin is given by
the transformation matrix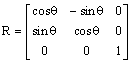 . Under this transformation,
points
. Under this transformation,
points ![]() and
and ![]() become
become 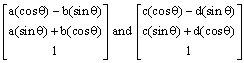 . When the distance
formula is applied to these points, one obtains
. When the distance
formula is applied to these points, one obtains ![]() .
.
11. By exercise #9,
distance is preserved under rotation, which forces angles to be preserved as
well. This may be verified using the
same approach used in exercise #9 applied to two points and their images under
translation. 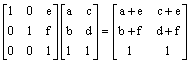 . Comparing distances
yields
. Comparing distances
yields ![]() . So, distance is
preserved under translation.
. So, distance is
preserved under translation.
Section 4.4
1.
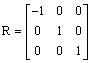
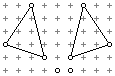
3.
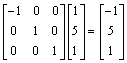
5.
Using matrix methods: 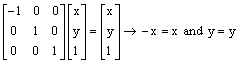 so all points
so all points ![]() are invariant, i.e.,
all point on the y-axis. To investigate
invariant lines, the line equation ku’ = uR-1 is used. In this case,
are invariant, i.e.,
all point on the y-axis. To investigate
invariant lines, the line equation ku’ = uR-1 is used. In this case,
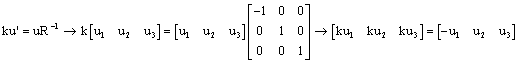 , so
, so
If k = 1, u1 = -u1
so u1 = 0, with u2 and u3 unconstrained. This leads to the line [0 u2 u3],
the set of horizontal lines in the plane.
If k = -1, then u2 = 0 = u3 , leading to the line
[u1 0 0], the y-axis.
Thinking geometrically, the reflecting
line x = 0 will be pointwise invariant.
Lines perpendicular to x = 0 will map onto themselves, crossing the
y-axis in the process. Each of these
lines are horizontal.
7.
Answers will vary.
9.
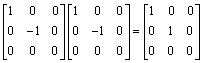
11. 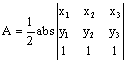 . Let
. Let 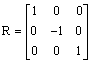 . Then
. Then 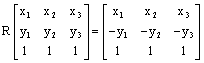 . But
. But 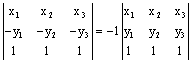 . Since the absolute
value function “removes” the negative sign, the areas will be the same.
. Since the absolute
value function “removes” the negative sign, the areas will be the same.
13.
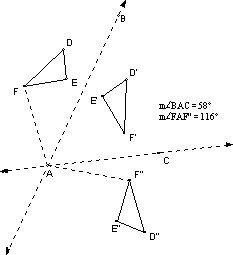
Section 4.5
1.
Using t, u, and v as translation vectors, we may write t+u = v.
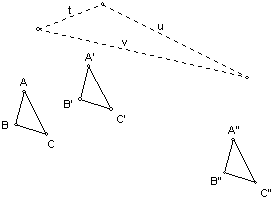
3.
With reflecting lines j and k parallel, we may show
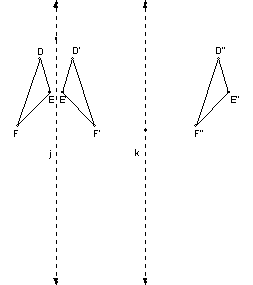
5.
a.
A reflection in the line y = x is given by the matrix  .
.
b. A reflection in
the line y = x+1 is given by the matrix 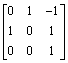
c.
A reflection in the line y = x+1 is given by the matrix 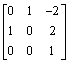
d. A reflection in
the line y = x-1 is given by the matrix 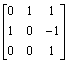
e.
A reflection in the line y = x-2 is given by the matrix 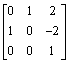
7.
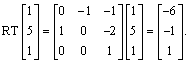
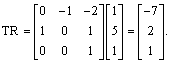 So the results are
not the same.
So the results are
not the same.
9.
The sequence of transformations is
a.
T1: Translate the reflecting line (and the plane in which it is
embedded) down 4 units to that the y-intercept becomes the origin
b. R1: Rotate the
reflecting line through an angle q = arctan(5) = 1.3734 radians to make it coincide with the x-axis
c.
F: Reflect the plane in the x-axis
d. R2: Rotate the
reflecting line through an angle -q = -arctan(5) = -1.3734 radians
e.
T2: Translate the reflecting line up 4 units to its original
position
Which is equivalent to T2*R2*F*R1*T1*X =
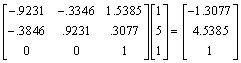
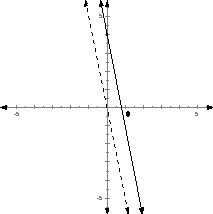
11. Let l = 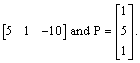 The steps in the
procedure are:
The steps in the
procedure are:
a.
T1: Translate P to the origin
b. R1: Rotate the
line 90 ° clockwise
c.
T2: Translate P back to its original position
Taking into consideration the manner in
which the line equation ku’ = uT-1 multiples lines by inverse
transformations, this sequence may be written as
l*T2*R1-1*T1
=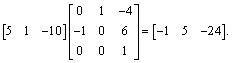
13.
a.
Invariant lines
i.
[u1 0 u3]
ii.
[0 u2 0] and [u1 0 u3]
iii.
[0 2u3 u3] and [u1 0 u3]
iv.
[0 -2u3 u3] and [u1 0 u3]
b. Eigen vectors
i.
[u1 0 u3]
ii.
[0 u2 0] and [u1 0 u3]
iii.
[0 2 u3 u3] and [u1 0 u3]
iv.
[0 -2u3 u3] and [u1 0 u3]
c.
The same, because eigenvectors always lie on invariant lines.
15.
Answers will vary.
Section 4.6
1.
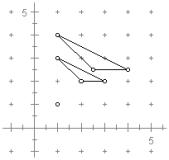
3.
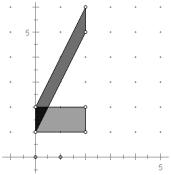
5.
a.
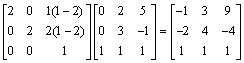
b.
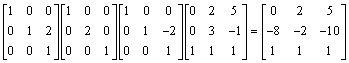
c.
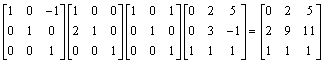
7.
![]() Answers will vary.
For instance,
Answers will vary.
For instance, 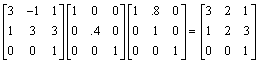
9.
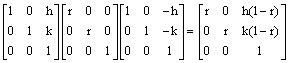
11.
![]()
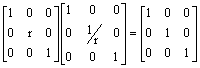
![]()
Section 5.1
1.
a.
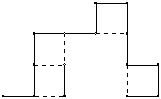
b.

3.
|
n |
r = # rows |
b = #boxes |
A = area of
1box |
Cumulative
Area |
|
0 |
1 |
1 |
1 |
1 = 1 |
|
1 |
4 = 3 +1 |
16 = 1+3+5+7 =
42 |
1/9 |
16(1/9) =
1.7777 |
|
2 |
13 = 32
+ 3 + 1 |
169 = 1+3+5+…+
23+25 = 132 |
(1/9)2 |
169(1/9)2
= 2.0864 |
|
3 |
40 =33
+ 32 + 3 + 1 |
1600 = 402 |
(1/9)3 |
1600(1/9)3
= 2.1948 |
5.
|
n |
#segments |
segment length |
curve length |
|
0 |
2 |
0.577350269 |
1.154700538 |
|
1 |
4 |
0.333333333 |
1.333333333 |
|
2 |
8 |
0.19245009 |
1.539600718 |
|
3 |
16 |
0.111111111 |
1.777777778 |
|
4 |
32 |
0.06415003 |
2.052800957 |
|
5 |
64 |
0.037037037 |
2.37037037 |
Section 5.2
1.
a.

b.
|
|
|
Section 5.3
1.
Consider two arbitrary points ![]() Let the distance
between these points be given by
Let the distance
between these points be given by ![]() . Since reversing the
order of the terms in each difference has no effect on the result,
. Since reversing the
order of the terms in each difference has no effect on the result, ![]() Since every pair of
points
Since every pair of
points ![]() has real, finite coordinates, the differences in the
x-coordinates is real and finite, as it the difference in the
y-coordinates. Consequently, the
computed distances are real and finite.
If a = b, then the difference terms for both x- and y-coordinates are
zero, hence the distance is zero. The
final point to be proven is that
has real, finite coordinates, the differences in the
x-coordinates is real and finite, as it the difference in the
y-coordinates. Consequently, the
computed distances are real and finite.
If a = b, then the difference terms for both x- and y-coordinates are
zero, hence the distance is zero. The
final point to be proven is that ![]() Assume
Assume ![]() for some set of
points a,b,c. Then
for some set of
points a,b,c. Then ![]() , which forces c to be closer to a than b. But it must also be true that
, which forces c to be closer to a than b. But it must also be true that ![]() , which forces c to be closer to b than a. Both of these statements cannot be true, so
the assumption is false. Consequently,
the triangle inequality holds in
, which forces c to be closer to b than a. Both of these statements cannot be true, so
the assumption is false. Consequently,
the triangle inequality holds in ![]()
3.
Answers will vary, but the result will not be a strange
attractor. In particular, it will not
be bounded.
5.
Change Map 3 to![]()
7.
a. The fixed point
is ![]() . A sequence of
iterates is given in the table below
. A sequence of
iterates is given in the table below
|
|
Seed
Point |
Fixed Point |
|
|
|
|
x-value |
1 |
-2 |
|
|
|
|
y-value |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
Iterate |
Old x-value |
New x-value |
Old y-value |
New y-value |
Distance from fixed point |
|
1 |
1 |
-0.5 |
1 |
1.5 |
1.58113883 |
|
2 |
-0.5 |
-1.25 |
1.5 |
1.75 |
0.790569415 |
|
3 |
-1.25 |
-1.625 |
1.75 |
1.875 |
0.395284708 |
|
4 |
-1.625 |
-1.8125 |
1.875 |
1.9375 |
0.197642354 |
|
5 |
-1.8125 |
-1.90625 |
1.9375 |
1.96875 |
0.098821177 |
|
6 |
-1.90625 |
-1.953125 |
1.96875 |
1.984375 |
0.049410588 |
|
7 |
-1.953125 |
-1.9765625 |
1.984375 |
1.9921875 |
0.024705294 |
|
8 |
-1.9765625 |
-1.9882813 |
1.9921875 |
1.99609375 |
0.012352647 |
|
9 |
-1.98828125 |
-1.9941406 |
1.99609375 |
1.998046875 |
0.006176324 |
|
10 |
-1.99414063 |
-1.9970703 |
1.99804688 |
1.999023438 |
0.003088162 |
b.
The fixed point is ![]() . A sequence of
iterates is given in the table below:
. A sequence of
iterates is given in the table below:
|
|
Seed
Point |
Fixed Point |
|
|
|
|
x-value |
1 |
-0.608365 |
|
|
|
|
y-value |
1 |
1.8718923 |
|
|
|
|
|
|
|
|
|
|
|
Iterate |
Old x-value |
New x-value |
Old y-value |
New y-value |
Distance from fixed point |
|
1 |
1 |
-0.06 |
1 |
2.05 |
0.576564416 |
|
2 |
-0.06 |
-0.545 |
2.05 |
2.0372 |
0.177036038 |
|
3 |
-0.545 |
-0.638672 |
2.0372 |
1.922834 |
0.059275383 |
|
4 |
-0.638672 |
-0.6276712 |
1.922834 |
1.87612892 |
0.019765623 |
|
5 |
-0.62767124 |
-0.6133278 |
1.87612892 |
1.868383977 |
0.006077614 |
|
6 |
-0.61332777 |
-0.6084454 |
1.86838398 |
1.869979089 |
0.0019149 |
|
7 |
-0.60844539 |
-0.6078836 |
1.86997909 |
1.87145296 |
0.00065171 |
|
8 |
-0.60788364 |
-0.6081545 |
1.87145296 |
1.871906414 |
0.000210975 |
|
9 |
-0.6081545 |
-0.6083266 |
1.87190641 |
1.871943877 |
6.43213E-05 |
|
10 |
-0.60832657 |
-0.6083707 |
1.87194388 |
1.871912542 |
2.10354E-05 |
Section 5.4
1.
a.
f(x) = x(1-x) ® x = x(1-x) ® x = 0 ® (0, 0) is a
fixed point.
b.
f(x) = 2x(1-x) ® x = 2x(1-x) ® both (0, 0) and
(.5, .5) are fixed points.
c.
f(x) = 3x(1-x) ® x = 3x(1-x) ® both (2/3, 2/3)
and (0, 0) are fixed points.
3.
Using the applet at URL 5.4.2, the following web diagrams may be
plotted.
a.
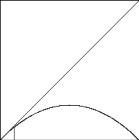
b.
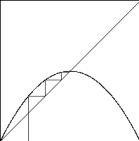
c.
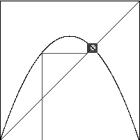
d.

Section 5.5
1.
![]() .
.
3.
a.
|
C Real |
C Imag |
Iterate |
Current R |
Current I |
New r |
New I |
|
0.5 |
-0.1 |
1 |
0 |
0 |
0.5 |
-0.1 |
|
|
|
2 |
0.5 |
-0.1 |
0.74 |
-0.2 |
|
|
|
3 |
0.74 |
-0.2 |
1.0076 |
-0.396 |
|
|
|
4 |
1.0076 |
-0.396 |
1.35844176 |
-0.8980192 |
|
|
|
5 |
1.35844176 |
-0.8980192 |
1.53892553 |
-2.5398136 |
|
|
|
6 |
1.53892553 |
-2.5398136 |
-3.5823612 |
-7.9171679 |
|
|
|
7 |
-3.5823612 |
-7.9171679 |
-49.348236 |
56.6243093 |
|
|
|
8 |
-49.348236 |
56.6243093 |
-770.56403 |
-5588.7195 |
|
|
|
9 |
-770.56403 |
-5588.7195 |
-30640017 |
8612932.37 |
|
|
|
10 |
-30640017 |
8612932.37 |
8.6463E+14 |
-5.278E+14 |
b.
|
C Real |
C Imag |
Iterate |
Current R |
Current I |
New r |
New I |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
|
2 |
1 |
0 |
2 |
0 |
|
|
|
3 |
2 |
0 |
5 |
0 |
|
|
|
4 |
5 |
0 |
26 |
0 |
|
|
|
5 |
26 |
0 |
677 |
0 |
|
|
|
6 |
677 |
0 |
458330 |
0 |
|
|
|
7 |
458330 |
0 |
2.1007E+11 |
0 |
|
|
|
8 |
2.1007E+11 |
0 |
4.4128E+22 |
0 |
|
|
|
9 |
4.4128E+22 |
0 |
1.9473E+45 |
0 |
|
|
|
10 |
1.9473E+45 |
0 |
3.7919E+90 |
0 |
c.
|
C Real |
C Imag |
Iterate |
Current R |
Current I |
New r |
New I |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
|
|
2 |
0 |
1 |
-1 |
1 |
|
|
|
3 |
-1 |
1 |
0 |
-1 |
|
|
|
4 |
0 |
-1 |
-1 |
1 |
|
|
|
5 |
-1 |
1 |
0 |
-1 |
|
|
|
6 |
0 |
-1 |
-1 |
1 |
|
|
|
7 |
-1 |
1 |
0 |
-1 |
|
|
|
8 |
0 |
-1 |
-1 |
1 |
|
|
|
9 |
-1 |
1 |
0 |
-1 |
|
|
|
10 |
0 |
-1 |
-1 |
1 |
d.
|
C Real |
C Imag |
Iterate |
Current R |
Current I |
New r |
New I |
|
1.414214 |
1.414214 |
1 |
0 |
0 |
1.41421356 |
1.41421356 |
|
|
|
2 |
1.41421356 |
1.41421356 |
1.41421356 |
5.41421356 |
|
|
|
3 |
1.41421356 |
5.41421356 |
-25.899495 |
16.7279221 |
|
|
|
4 |
-25.899495 |
16.7279221 |
392.374675 |
-865.07525 |
|
|
|
5 |
392.374675 |
-865.07525 |
-594395.89 |
-678865.83 |
|
|
|
6 |
-594395.89 |
-678865.83 |
-1.076E+11 |
8.0703E+11 |
|
|
|
7 |
-1.076E+11 |
8.0703E+11 |
-6.397E+23 |
-1.736E+23 |
|
|
|
8 |
-6.397E+23 |
-1.736E+23 |
3.7912E+47 |
2.2211E+47 |
|
|
|
9 |
3.7912E+47 |
2.2211E+47 |
9.4399E+94 |
1.6841E+95 |
|
|
|
10 |
9.4399E+94 |
1.6841E+95 |
-1.95E+190 |
3.18E+190 |
e.
|
C Real |
C Imag |
Iterate |
Current R |
Current I |
New r |
New I |
|
2 |
1 |
1 |
0 |
0 |
2 |
1 |
|
|
|
2 |
2 |
1 |
5 |
5 |
|
|
|
3 |
5 |
5 |
2 |
51 |
|
|
|
4 |
2 |
51 |
-2595 |
205 |
|
|
|
5 |
-2595 |
205 |
6692002 |
-1063949 |
|
|
|
6 |
6692002 |
-1063949 |
4.3651E+13 |
-1.424E+13 |
|
|
|
7 |
4.3651E+13 |
-1.424E+13 |
1.7026E+27 |
-1.243E+27 |
|
|
|
8 |
1.7026E+27 |
-1.243E+27 |
1.3535E+54 |
-4.233E+54 |
|
|
|
9 |
1.3535E+54 |
-4.233E+54 |
-1.61E+109 |
-1.15E+109 |
|
|
|
10 |
-1.61E+109 |
-1.15E+109 |
1.275E+218 |
3.687E+218 |
Section
6.1
1.
a.
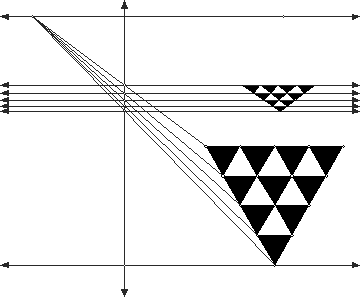
3.
Answers
will vary.
Section
6.2
1.
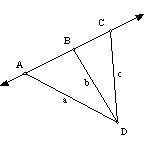
3.
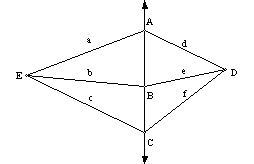
5.
a.
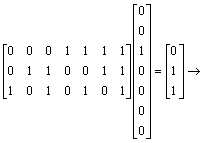 It is not a code
word.
It is not a code
word.
b.
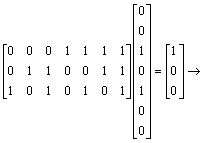 It is not a code word.
It is not a code word.
c.
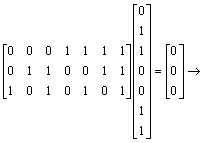 It is a code word.
It is a code word.
7.
|
|
A
complete quadrangle consists of 4 points and the 6 lines they determine. In this order 2 finite projective plane,
every combination of 4 vertices is examined to see if the necessary lines
exist. If not, the combination of
points is crossed through. Five
complete quadrangles remain.
ABCG ABDE BCEF
ACDF
By duality, five complete quadrilaterals
exist. |
Section
6.3
1.
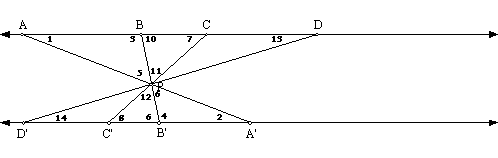
Since
![]() By vertical angles,
By vertical angles, ![]() Then
Then ![]() Consequently,
Consequently, ![]() Similarly,
Similarly, ![]()
![]() Then
Then ![]() . So,
. So, 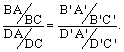
3.
If
concurrent lines k and l separate lines m and n harmonically, the rays form a
harmonic set.
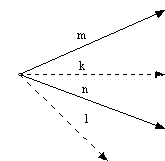
5.
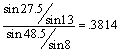
Section 6.4
1.
When the points are collinear.
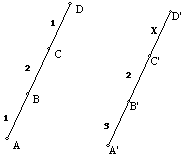
3.
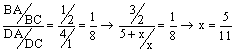 .
.
Section 6.5
1.
a.
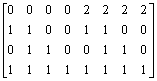
b.
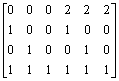
3.
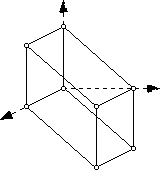
5.
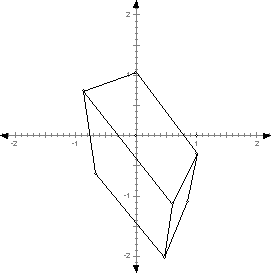
Section 6.6
Section 6.7
1.
![]()