Triangle Investigation

 

Contents

  Problem Statement 

  Key Mathematical Concepts 

  Approach 

  Principle Findings and Results: 

  Area 
  Segments 
  Angles
 

  Related Site

http://jwilson.coe.uga.edu/emt669/essays/concurrent.html

Problem Statement

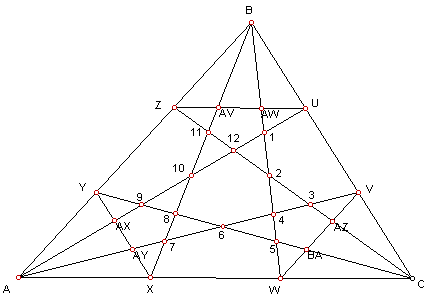
Given a triangle in which line segments are constructed, by connecting each vertex to the opposite sides’ trisection points, make as many observations as possible, concerning various areas, angles, and segments. State a formal conjecture for each of the observations and prove at least one of them. 

 

Key Mathematical Concepts

Formal Geometric Proofs 

Invariance of areas under transformation 

Invariance of the ratios of segments, areas, and angles under transformation 

Approach

The basic approach is one of "play". Make a guess about some relationship that might be true. Use the calculator to list a measurement or ratio of measurements. Drag a vertex around, causing the triangle to cycle from acute to obtuse. Do the same with each vertex. If the listed measurement remains constant, then the relationship selected is invariant. The following observations will be divided into areas, segments, and angles. 

 

Principal Findings and Results

Area:

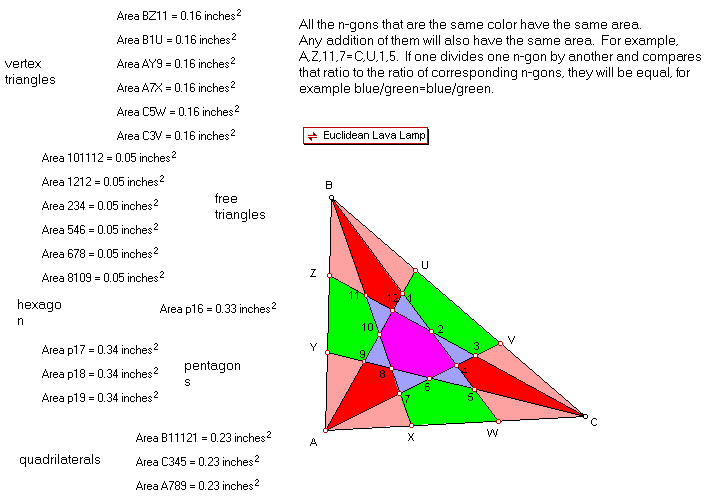
The triangle contains four primary shapes: 

  1. hexagon- 2,4,6,8,10,12
  2. pentagons- U123V= XW567= ZY9,10,11
  3. vertex triangles- BZ,11= BU1= AY9= A7X= 5WC= CV3
  4. free triangles- 10,11,12= 12,1,2= 2,3,4= 4,5,6= 6,7,8= 8,9,10
  5. quadrilaterals- B,10,11,1= A987= C345

 

 

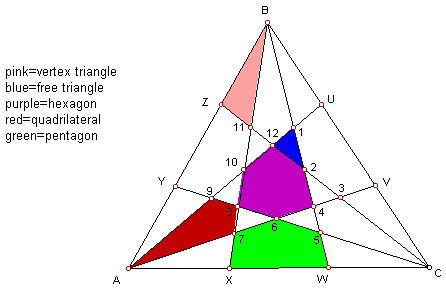
All other shapes are obtainable by adding various combinations of the above five shapes. 

All pentagons have the same area. All vertex triangles have the same area. All free triangles have the same area. All quadrilaterals have the same area. Like combinations, (for example CYA=UAB, three vertex triangles plus a pentagon plus a free triangle plus a quadrilateral), will have the same area. 

 

 

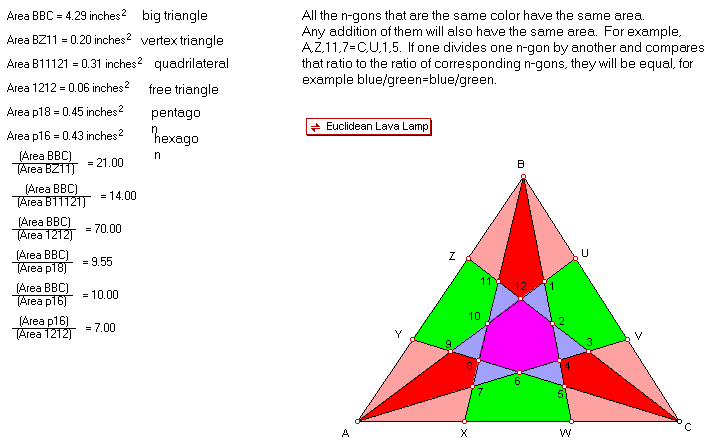
Ratio of Areas: 

Triangle ABC divided by a hexagon = 10. 

Triangle ABC divided by a pentagon = 9.55. 

Triangle ABC divided by a vertex triangle = 21. 

Triangle ABC divided by a free triangle = 70. 

Triangle ABC divided by a quadrilateral = 14. 

Also the various permutations of the different figures above are obtainable 

(for example, hexagon divided by free triangle = 7). 

 

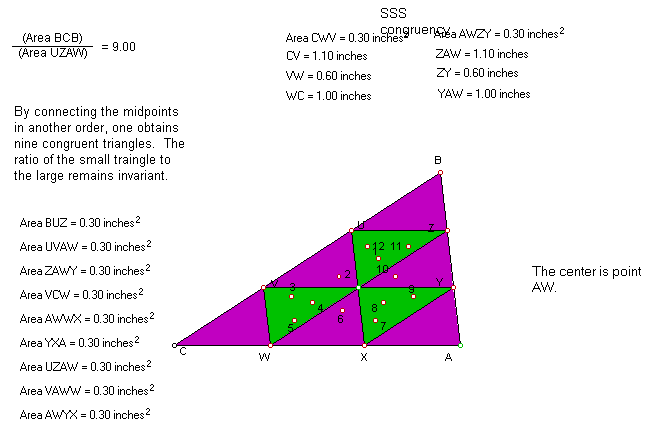
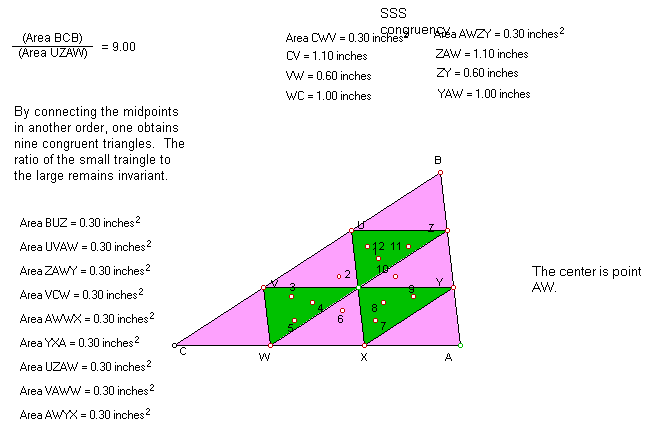
If one constructs segments ZU, YX, and VW: 

a) Triangles BZU, YAX, VWC, UVAW, ZAWY, AWWX, UZAW, VAWW, and AWYX are congruent, so their areas are equal. 

 

b) Additionally, three stars are formed which are of equal areas- 

B,AV,Z,11,10,12,2,1,U,AW 

10,9,Y,AX,A,AY,X,7,6,8 

2,4,6,5,W,BA,C,AZ,V,3 

  

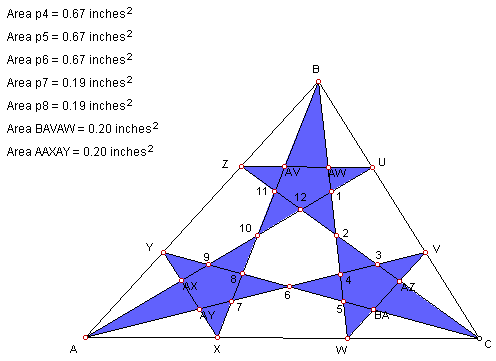
With additional segments created, more triangles can be found to have equal areas: 
ZUV, VXW, XZY and YUV, UWX, WZY. 

 

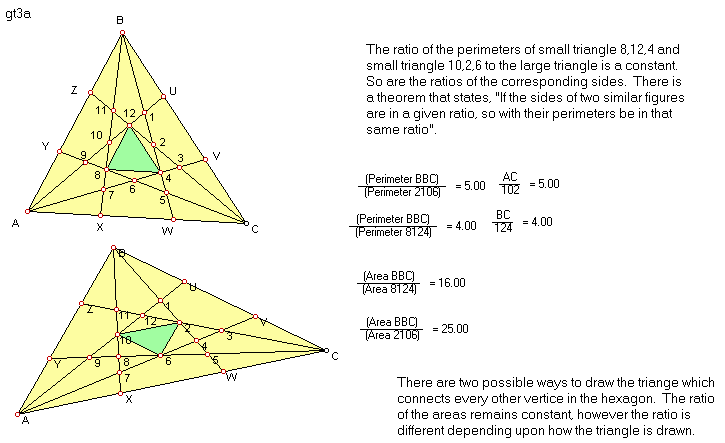
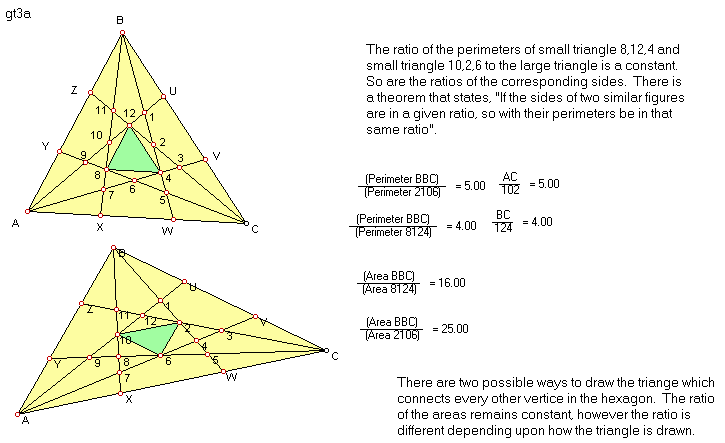
The hexagon can make two triangles inside it, by connecting every other vertex. The ratio of the area of these triangles to the larger triangle remains invariant under transformation. 

 

 

Segments:

There are three sets of eight parallel lines in the triangle 

Any two sets of corresponding parallel lines are in equal ratios. 

 

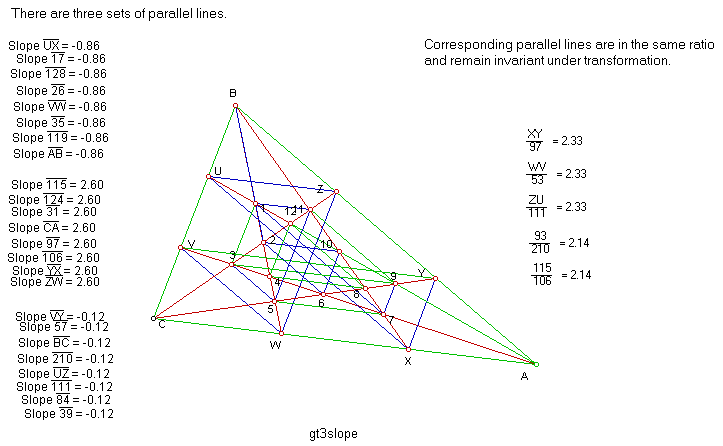
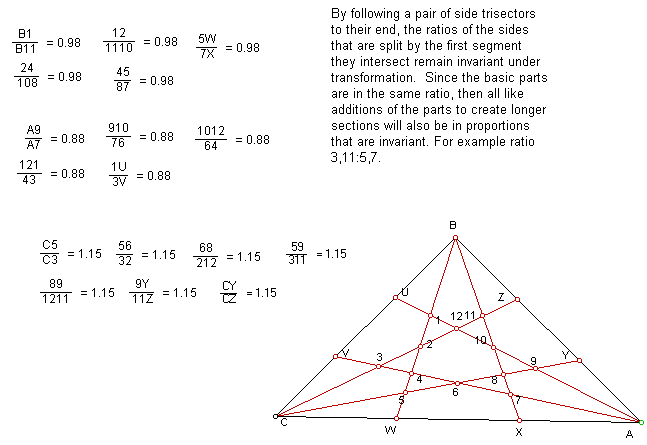
By following a pair of trisectors to their end, the ratios of the sides that are split by the first segment they intersect remain invariant under transformation. Since the basic parts are in the same ratio, then all like additions of the parts, to create longer sections will also be in proportions that are invariant. 

 

The ratio of the perimeter of the triangles contained within the hexagon to the large triangle remains invariant under transformation. 

 

The perimeters and the corresponding sides of the nine congruent triangles are equal.  

 

 

Angles:

For all the above sketches, if two or more figures are said to be similar or congruent, then their corresponding angles are congruent. All vertical angles are congruent to each other. In the parallel sketch alternate interior and exterior angles are congruent, as are corresponding angles.