Saccheri Quadrilaterals
Problem Statement:
I. Using the labeled diagram prove that in a Saccheri quadrilateral that
- The summit angles are acute and congruent.
- The summit is longer than the base
II. Prove for any hyperbolic triangle, the sum of the angles is less than 180 degrees.

Strategic Plan and/or Approach:
To prove that the summit angles are acute and congruent, given the Saccheri quadrilateral above, we did the following constructions:
First, we made infinite line AB, then constructed circles AB and BA, then constructed perpendiculars through B to AB and through A to AB. This results are right angles for ABE and BAH. It also makes segments BE and AH congruent. The summit is segment EH and the base is segment AB.
The measure of angle HIW is greater than the measure of angle EHW because of Thm. 9.4, which states that for any omega triangle the measure of the exterior angle is greater than the opposite interior. Since the measure of angle EBW equals HAW , then the measure of angle AHI is greater than BEH. But the measure of angle BEH equals the measure of angle AHE and therefore the measure of angle AHI is greater than AHE so AHE is acute. This argument is then repeated for the other summit angle with J taking the place of I and swapping in all the corresponding parts. The measurements in the sketch above provide further confirmation.
To prove that the summit is longer than the base, we used the following diagram:
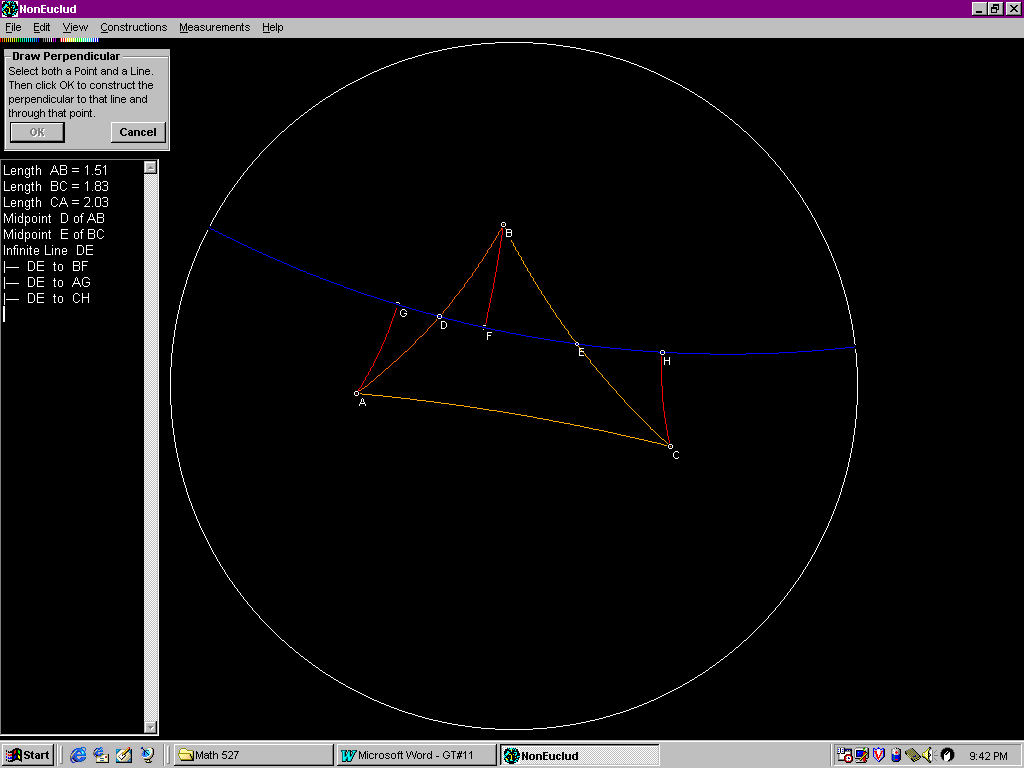
By looking at the Saccheri quadrilateral ACHG, we want to show that the summit, AC, is longer than the base, HG. We know that the shortest distance from a point to a line is a perpendicular segment. In hyperbolic space, the shortest distance from a point A on line n to a line m is a perpendicular line and the shortest distance from a point B on line m to a line n is a different perpendicular line. Therefore a common line that is both the shortest distance from A to line m and from B to line n is one that is perpendicular to both. This is the shortest distance. By looking at the preceding diagram, we find that G is perpendicular to CH and H is perpendicular to AG. Therefore, GH is the shortest line between segments AG and CH. This is because if there were another "shortest line" then there would be four right angles, and that would create a rectangle (which is not possible in hyperbolic space). Therefore, since GH (base) is the shortest line between segments AG and CH, then AC (summit) must be longer.
To prove that for any hyperbolic triangle, the sum of the angles is less than 180 degrees we considered the following diagram:
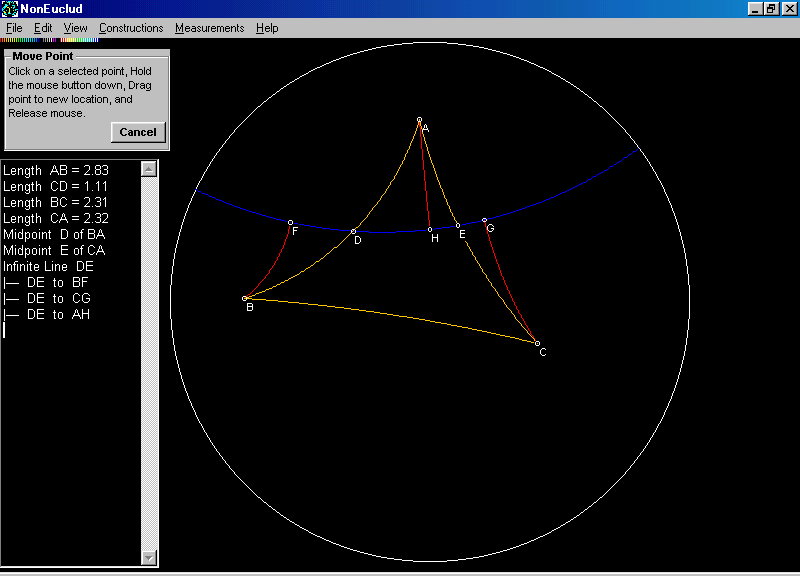
Consider that triangle ABC is an arbitrary hyperbolic triangle with base BC. Let D and E be the midpoints of the sides AB and BC. Let BF, AH, and CG be the perpendiculars to the infinite line ED from points B, C, and A. Since < BDF is congruent to <ADH this means the Triangle BDF is congruent to Triangle ADH and also <FBD is congruent to Angle HAD and segment BF is congruent to segment AH. Also angle GCE is congruent to angle HAE and segment AH is congruent to segment CG. Therefore BF is congruent to segment CG, and quadrilateral BFGC is a Saccheri quadrilateral. Since we have proven in part I that the summit angles of a Saccheri quadrilateral are congruent and acute. <FBC is congruent to <GCB and both are acute, so their sum has to be less than 180 degrees. Also we know that <FBC + <GCB = <FBD + <DBC + <GCE + ECB
= <HAB + <ABC + <HAE + <ACB
= <ABC + <BAC + ACB
Therefore the sum of the angles of triangle ABC is less than 180 degrees