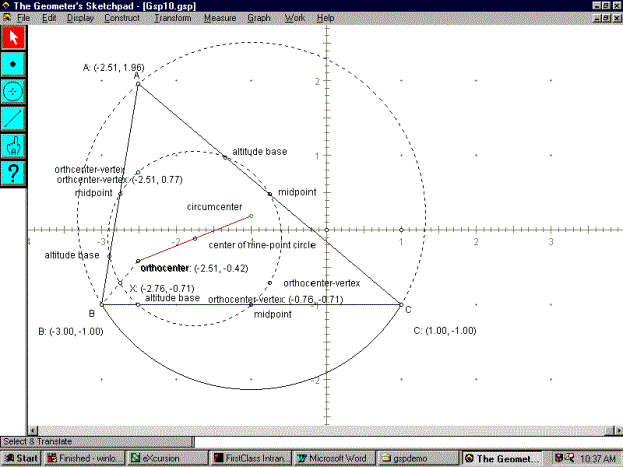
Problem
Statement
Using analytic geometry and as much matrix notation as you
can employ, show that the nine-point circle and the circumcircle are related
by a linear transformation, a dilation using the orthocenter as the center of
the dilation and a scaling factor of 1/2. The transformation matrix for a
dilation with center (c1, c2, 1) and ratio r is
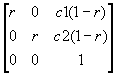 . .
Approach
First of all, we used the orthocenter as our center for
dialation. In our equation, this was the point:
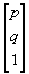
Since the scaling factor was ½, that is what we plugged in
for r in the transformation matrix. Next, we multiplied the transformation
matrix,
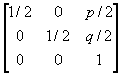
by a set of three points
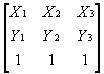
which are the points that are the vertices of the triangle
that intersect the circumcircle. This gave us three image points on the nine
point circle. They are of the form
. 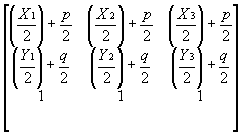
This matrix would seem logical since we are looking at the
midpoint of the orthocenter (p,q) and the points on the circumcircle (X,Y).
Their sum divided by 2 illustrates the midpoint of the
segment.
|